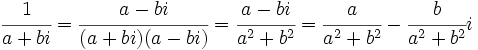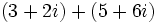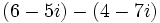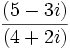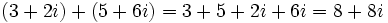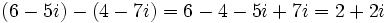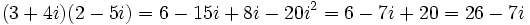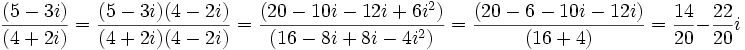Números complejos: Operaciones (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:18 5 mar 2009 Coordinador (Discusión | contribuciones) (→Operaciones con números complejos en forma binómica) ← Ir a diferencia anterior |
Revisión de 17:27 5 mar 2009 Coordinador (Discusión | contribuciones) (→Operaciones con números complejos en forma binómica) Ir a siguiente diferencia → |
||
| Línea 16: | Línea 16: | ||
| {{ejemplo | {{ejemplo | ||
| |titulo=Ejemplos: ''Operaciones con complejos en forma binómica'' | |titulo=Ejemplos: ''Operaciones con complejos en forma binómica'' | ||
| - | |enunciado=Efectúa las siguientes operaciones: | + | |enunciado=:Efectúa las siguientes operaciones: |
| - | :* <math>\,(3 + 2i) + (5 + 6i)</math> | + | :# <math>\,(3 + 2i) + (5 + 6i)</math> |
| - | :* <math>\,(6 - 5i) - (4 - 7i)</math> | + | :# <math>\,(6 - 5i) - (4 - 7i)</math> |
| - | :* <math>\,(3 + 4i) (2 - 5i)</math> | + | :# <math>\,(3 + 4i) (2 - 5i)</math> |
| - | :* <math>\,\frac{(5 - 3i)}{(4 + 2i)}</math> | + | :# <math>\,\frac{(5 - 3i)}{(4 + 2i)}</math> |
| |sol= | |sol= | ||
| - | :* <math>\,(3 + 2i) + (5 + 6i)=3 + 5 + 2i + 6i=8 + 8i</math> | + | # <math>\,(3 + 2i) + (5 + 6i)=3 + 5 + 2i + 6i=8 + 8i</math> |
| - | :* <math>\,(6 - 5i) - (4 - 7i)=6-4-5i+7i=2+2i</math> | + | # <math>\,(6 - 5i) - (4 - 7i)=6-4-5i+7i=2+2i</math> |
| - | :* <math>\,(3 + 4i) (2 - 5i)=6-15i+8i-20i^2=6-7i+20=26-7i</math> | + | # <math>\,(3 + 4i) (2 - 5i)=6-15i+8i-20i^2=6-7i+20=26-7i</math> |
| - | :* <math>\,\frac{(5 - 3i)}{(4 + 2i)}=\frac{(5 - 3i)(4-2i)}{(4 + 2i)(4-2i)}=\frac{(20-10i-12i+6i^2)}{(16-8i+8i-4i^2)}=\frac{(20-6-10i-12i)}{(16+4)}=\frac{14}{20}-\frac{22}{20}i</math> | + | # <math>\,\frac{(5 - 3i)}{(4 + 2i)}=\frac{(5 - 3i)(4-2i)}{(4 + 2i)(4-2i)}=\frac{(20-10i-12i+6i^2)}{(16-8i+8i-4i^2)}=\frac{(20-6-10i-12i)}{(16+4)}=\frac{14}{20}-\frac{22}{20}i</math> |
| }} | }} | ||
| - | + | {{p}} | |
| + | ==Propiedades de las operaciones con números complejos== | ||
| + | {{Caja_Amarilla|texto= | ||
| + | :* El 0 es el '''elemento neutro''' de la '''suma'''. | ||
| + | :* Todo número complejo, <math>a+bi\,</math>, tiene un '''opuesto''', <math>-a-bi\,</math> | ||
| + | :* El 1 es el '''elemento neutro''' del producto. | ||
| + | :* Todo número complejo, <math>a+bi\,</math>, distinto de 0, tiene '''inverso''', <math>\cfrac{1}{a+bi}</math>: | ||
| + | <center><math>\cfrac{1}{a+bi}=\cfrac{a-bi}{(a+bi)(a-bi)}=\cfrac{a-bi}{a^2+b^2}=\cfrac{a}{a^2+b^2}-\cfrac{b}{a^2+b^2}i</math></center>}} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | [[Categoría: Matemáticas]][[Categoría: Geometría]][[Categoría: Números]] | ||
Revisión de 17:27 5 mar 2009
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Operaciones con números complejos en forma binómica
- Suma:
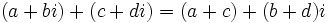
- Resta:
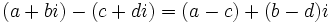
- Multiplicación:
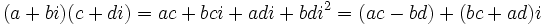
- División:
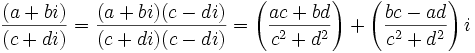 , siempre que
, siempre que 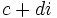 no sea nulo.
no sea nulo.
- Suma:
Propiedades de las operaciones con números complejos
- El 0 es el elemento neutro de la suma.
- Todo número complejo,
 , tiene un opuesto,
, tiene un opuesto, 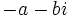
- El 1 es el elemento neutro del producto.
- Todo número complejo,
 , distinto de 0, tiene inverso,
, distinto de 0, tiene inverso, 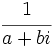 :
: