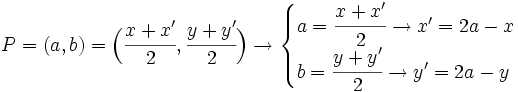Puntos y vectores el plano (1ºBach)
De Wikipedia
| Revisión de 13:36 17 mar 2009 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 13:38 17 mar 2009 Coordinador (Discusión | contribuciones) (→Simétrico de un punto respecto de otro) Ir a siguiente diferencia → |
||
| Línea 225: | Línea 225: | ||
| <center><math>M=\Big( \cfrac{2+7}{2}, \cfrac{4+2}{2} \Big)=(4.5,3)</math></center> | <center><math>M=\Big( \cfrac{2+7}{2}, \cfrac{4+2}{2} \Big)=(4.5,3)</math></center> | ||
| - | Moviendo con el ratón los puntos A y/o B podrás comprobar cuáles son las coordenadas del punto medio M, de cualquier otro segmento AB. | + | Moviendo con el ratón los puntos A y/o B podrás comprobar cuáles son las coordenadas del punto medio M, de cualquier otro segmento AB. También te vale para comprobar el punto simétrico de otro punto respecto de uno dado. |
| <center><iframe> | <center><iframe> | ||
| Línea 238: | Línea 238: | ||
| #Calcula en tu cuaderno las coordenadas del punto medio del segmento de extremos A(-3,7), B(7,-1). Comprueba el resultado en la escena anterior. | #Calcula en tu cuaderno las coordenadas del punto medio del segmento de extremos A(-3,7), B(7,-1). Comprueba el resultado en la escena anterior. | ||
| - | #Calcula en tu cuaderno el simétrico, P', del punto P(8,4) respecto de Q(4,1) | + | #Calcula en tu cuaderno el simétrico, P', del punto P(8,4) respecto de Q(4,1). Compruébalo en la escena. |
| }} | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Geometría]] | [[Categoría: Matemáticas]][[Categoría: Geometría]] | ||
Revisión de 13:38 17 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Sistema de referencia en el plano
Un sistema de referencia del plano consiste en una terna 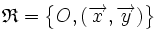 , donde
, donde  es un punto fijo, llamado origen, y
es un punto fijo, llamado origen, y 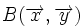 una base de vectores del plano.
una base de vectores del plano.
En este sistema de referencia, cada punto  del plano tiene asociado un vector fijo
del plano tiene asociado un vector fijo 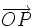 , llamado vector de posición del punto
, llamado vector de posición del punto  .
.
Si el vector 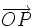 tiene coordenadas
tiene coordenadas 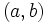 respecto de la base
respecto de la base 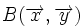 , el punto
, el punto  diremos que tiene coordenadas
diremos que tiene coordenadas 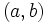 respecto del sistema de referencia
respecto del sistema de referencia 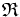 .
.
Normalmente trabajaremos con un sistema de referencia en el que la base es ortonormal.
|
Actividad interactiva: Sistema de referencia en el plano
Actividad: En la siguiente escena tenemos un punto  que da lugar al vector que da lugar al vector 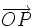 , que tiene de coordenadas , que tiene de coordenadas 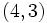 respecto de la base ortonormal respecto de la base ortonormal 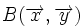 . .
Así, el punto Ejercicio:
|
Coordenadas del vector que une dos puntos
|
Actividad interactiva: Coordenadas del vector que une dos puntos
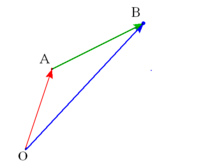
Actividad: En la siguiente escena tenemos dos puntos 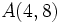 y y 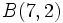 . .
Las coordenadas del vector Ejercicio:
|
Condición para que tres puntos estén alineados
Condición para que tres puntos estén alineados
- Los puntos del plano
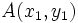 ,
, 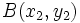 y
y 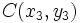 , están alineados si se cumple:
, están alineados si se cumple:
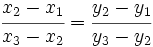
Los puntos del plano 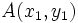 ,
, 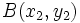 y
y 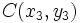 , están alineados si los vectores
, están alineados si los vectores 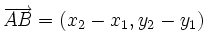 y
y 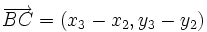 tienen la misma dirección.
tienen la misma dirección.
Ahora, esto ocurre si los vectores son proporcionales: 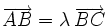
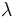 , se obtiene lo que buscamos.
, se obtiene lo que buscamos.|
Actividad interactiva: Condición para que tres puntos estén alineados Actividad 1: Comprobación de que tres puntos del plano están alineados en un sistema de referencia ortonormal . Actividad: En esta escena puedes mover los puntos B y C, para comprobar que las coordenadas de los vectores AB y BC son proporcionales, ya que los puntos A, B y C están alineados. Anota en tu cuaderno las coordenadas de A, B y C, la de los vectores AB y BC y la proporción entre las x y las y en el inicio de la escena. Ejercicio:
Actividad 2: Averigua las coordenadas de un punto para que esté alineado con otros dos. Actividad: En esta escena tenemos tres puntos P(1,4), Q(5,-2) y R(m,n) Moviendo adecuadamente el punto R, o cambiando los valores de m y/o n, puedes conseguir que los puntos P, Q y R estén en la misma recta azul, o sea, ALINEADOS.
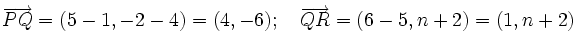 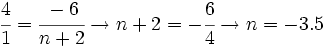 Ejercicio:
|
Punto medio de un segmento
Simétrico de un punto respecto de otro
|
Actividad interactiva: Punto medio y punto simétrico
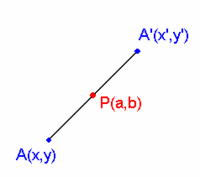
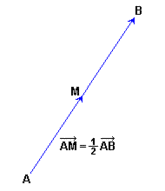
Actividad: En la siguiente escena tenemos el punto medio de un segmento de extremos 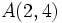 y y 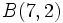 . .
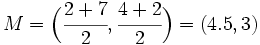 Moviendo con el ratón los puntos A y/o B podrás comprobar cuáles son las coordenadas del punto medio M, de cualquier otro segmento AB. También te vale para comprobar el punto simétrico de otro punto respecto de uno dado. Ejercicios:
|
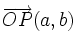
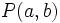 .
.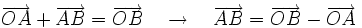
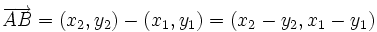
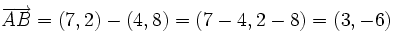
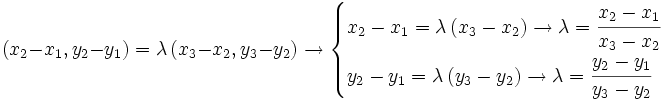
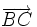
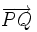
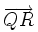
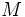 , de un segmento de extremos
, de un segmento de extremos 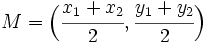
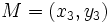 el punto medio del segmento
el punto medio del segmento 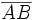
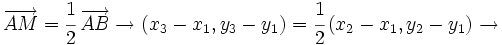
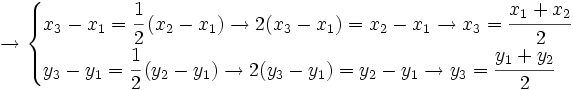
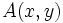 respecto del punto
respecto del punto  .
.