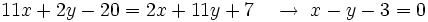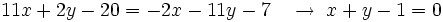Lugares geométricos (1ºBach)
De Wikipedia
| Revisión de 17:48 23 mar 2009 Coordinador (Discusión | contribuciones) (→Bisectriz de un ángulo) ← Ir a diferencia anterior |
Revisión de 17:50 23 mar 2009 Coordinador (Discusión | contribuciones) (→Lugar geométrico) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | Vamos a estudiar a continuación algunos lugares geométricos como la mediatriz de un segmento, la bisectriz de un ángulo o la circunferencia. En todos estos casos buscaremos una ecuación que describa a dicho lugar geométrico. | + | Vamos a estudiar a continuación algunos lugares geométricos como la mediatriz de un segmento o la bisectriz de un ángulo. En cada caso buscaremos una ecuación que describa a dicho lugar geométrico. |
| {{p}} | {{p}} | ||
| + | |||
| ==Mediatriz de un segmento== | ==Mediatriz de un segmento== | ||
| {{Caja_Amarilla|texto= La '''mediatriz de un segmento''' <math>\overline{AB}</math>, es el lugar geométrico de los puntos <math>X\,</math>, que equidistan de los extremos <math>A\,</math> y <math>B\,</math>. | {{Caja_Amarilla|texto= La '''mediatriz de un segmento''' <math>\overline{AB}</math>, es el lugar geométrico de los puntos <math>X\,</math>, que equidistan de los extremos <math>A\,</math> y <math>B\,</math>. | ||
Revisión de 17:50 23 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Lugar geométrico
Se llama lugar geométrico a un conjunto de puntos que cumplen una cierta propiedad.
Vamos a estudiar a continuación algunos lugares geométricos como la mediatriz de un segmento o la bisectriz de un ángulo. En cada caso buscaremos una ecuación que describa a dicho lugar geométrico.
Mediatriz de un segmento
La mediatriz de un segmento 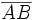 , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 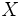 , que equidistan de los extremos
, que equidistan de los extremos 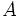 y
y 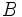 .
.
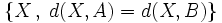
|
Actividad interactiva: Mediatriz de un segmento
Actividad 1: En la siguiente escena hallaremos la ecuación de la mediatriz del segmento de extremos
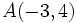 y y 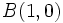 y la representaremos gráficamente. y la representaremos gráficamente.Actividad: Para hallar la ecuación del lugar geométrico 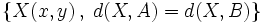 escribiremos la fórmula de la distancia entre dos puntos: 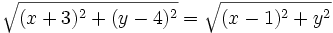 Elevando ambos miembros al cuadrado, desarrollando los cuadrados de los binomios y simplificando, comprueba que queda la ecuación: 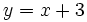 Por tanto, la mediatriz del segmento es una recta.
|
Bisectriz de un ángulo
La bisectriz de un ángulo de lados  y
y 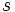 , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 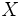 , que equidistan de los lados xtremos
, que equidistan de los lados xtremos  y
y 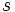 .
.
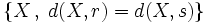
|
Actividad interactiva: Bisectriz de un ángulo
Actividad 1: En la siguiente escena hallaremos la ecuación de la bisectriz del ángulo que forman las rectas
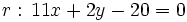 y y 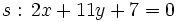 , y la representaremos gráficamente. , y la representaremos gráficamente.Actividad: Para hallar la ecuación del lugar geométrico 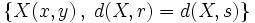 escribiremos la fórmula de la distancia de un punto a una recta: 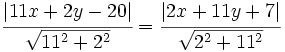 De aquí salen dos ecuaciones, ya que si Así, las dos ecuaciones resultantes son: o bien Por tanto la bisectriz de un ángulo es una recta, o mejor dicho, un par de rectas perpendiculares. En la siguiente escena tienes representadas en rojo la segunda y en gris la primera.
|
Circunferencia
La circunferencia de centro  y radio
y radio  , es el lugar geométrico de los puntos
, es el lugar geométrico de los puntos 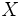 , cuya distancia al centro es
, cuya distancia al centro es  .
.
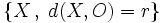
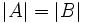 , se puede dar que
, se puede dar que 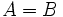 o que
o que 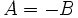 :
: