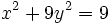La hipérbola (1ºBach)
De Wikipedia
| Revisión de 18:55 31 mar 2009 Coordinador (Discusión | contribuciones) (→Elementos de la hipérbola) ← Ir a diferencia anterior |
Revisión de 19:05 31 mar 2009 Coordinador (Discusión | contribuciones) (→Excentricidad de la elipse) Ir a siguiente diferencia → |
||
| Línea 35: | Línea 35: | ||
| {{p}} | {{p}} | ||
| - | ==Excentricidad de la elipse== | + | ==Excentricidad de la hipérbola== |
| - | {{Caja Amarilla|texto=La '''escentricidad''' es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. | + | {{Caja Amarilla|texto=La '''excentricidad''' es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia. |
| - | La excentricidad de la elipse es el cociente entre la distancia focal y el eje mayor: | + | La excentricidad de la hipérbola es el cociente entre la distancia focal y el eje: |
| <center><math>e=\cfrac{c}{a}</math></center> | <center><math>e=\cfrac{c}{a}</math></center> | ||
| Línea 45: | Línea 45: | ||
| {{p}} | {{p}} | ||
| {{Teorema|titulo=Propiedades|enunciado= | {{Teorema|titulo=Propiedades|enunciado= | ||
| - | *<math>0<e<1\,</math>. | + | :En una hipérbola <math>e>1\,</math>. |
| - | *Una elipse más se parece a a una circunferencia, cuanto más se aproxime a 0 su excentricidad. | + | |
| |demo= | |demo= | ||
| - | *Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que <math>a>c \rightarrow \cfrac{c}{a}<1</math> | + | *Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que <math>c>a \rightarrow \cfrac{c}{a}>1</math> |
| - | + | ||
| - | :y como <math>a>0\,</math> y <math>c>0\,</math>, tenemos que <math>\cfrac{c}{a}>0</math> | + | |
| - | + | ||
| - | *Cuanto más próxima a 0 sea la excentricidad, más proximo a cero estará <math>c\,</math> (la distancia focal se aproximará a cero) y <math>a\,</math> se aproximará a <math>b\,</math>. Así, la elipse, se aproximará a una circunferencia de centro los focos y radio <math>a=b\,</math>. | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{AI2|titulo=Actividad interactiva: ''Excentricidad de la elipse''|cuerpo= | + | {{AI2|titulo=Actividad interactiva: ''Excentricidad de la hipérbola''|cuerpo= |
| {{ai_cuerpo | {{ai_cuerpo | ||
| - | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver como se ve afectada la elipse si modificamos su excentricidad. | + | |enunciado='''Actividad 1:''' En la siguiente escena vamos a ver como se ve afectada la hipérbola si modificamos su excentricidad. |
| |actividad= | |actividad= | ||
| <center><iframe> | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/geogebra/figuras/elipse_4.html | + | url=http://maralboran.org/web_ma/geogebra/figuras/hiperbola_4.html |
| width=780 | width=780 | ||
| height=460 | height=460 | ||
| name=myframe | name=myframe | ||
| </iframe></center> | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/geogebra/figuras/elipse_4.html '''Click''' aquí si no se ve bien la escena]</center> | + | <center>[http://maralboran.org/web_ma/geogebra/figuras/hiperbola_4.html '''Click''' aquí si no se ve bien la escena]</center> |
| '''Ejercicios:''' | '''Ejercicios:''' | ||
| - | #¿A qué se le llama excentricidad de una elipse? ¿Es correcto el valor de la excentricidad de la elipse de la figura? | + | Modifica el valor de e (deslizando el punto verde) y observa los cambios. |
| - | #Modifica el valor de e (deslizando el punto verde) y observa los cambios. | + | |
| - | ##¿Entre qué valores puede variar la excentricidad de una elipse? | + | * ¿Entre qué valores puede variar la excentricidad de una hipérbola? |
| - | ##¿Cómo son las elipses de excentricidad grande (próxima a 1)? ¿Y la elipse de excentricidad 0? | + | * ¿Cómo son las hipérbola de excentricidad grande? ¿y las de poca excentricidad (próxima a 1)? |
| - | ##¿Sabías que la Tierra da vueltas alrededor del Sol describiendo una órbita elíptica de excentricidad 0.016751? Aproxima a ese valor el de la excentricidad de la elipse de la figura. ¿Describe la figura resultante. ¿Dónde crees que se sitúa el Sol? | + | * Intenta visualizar una '''hipérbola equilátera''' (asíntotas perpendiculares). ¿Cuál es su excentricidad? ¿Sabrías demostrarlo? |
| - | ##Los planetas de nuestro Sistema Solar cuya órbita tiene mayor excentricidad son Marte (e=0.09) y Plutón (e=0.25). Comprueba qué aspecto tiene dichas órbitas. | + | |
| - | #Pulsa el botón Actualizar para recuperar la imagen inicial. Modifica el valor de a y observa los cambios. | + | Pulsa el botón Actualizar para recuperar la imagen inicial. Modifica el valor de a y observa los cambios. |
| - | ##¿Qué tienen en común todas las elipses con la misma excentricidad? | + | |
| + | * ¿Qué tienen en común todas las hipérbolas con la misma excentricidad? | ||
| + | |||
| }} | }} | ||
| }} | }} | ||
Revisión de 19:05 31 mar 2009
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
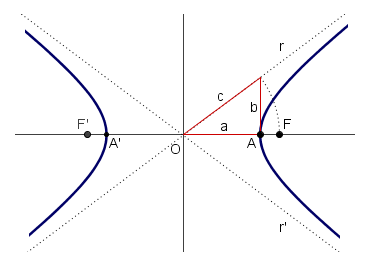
Elementos de la hipérbola
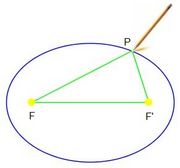
Una una elipse de focos
| 
|
Excentricidad de la hipérbola
La excentricidad es un parámetro que determina el grado de desviación de una sección cónica con respecto a una circunferencia.
La excentricidad de la hipérbola es el cociente entre la distancia focal y el eje:
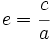
Propiedades
- En una hipérbola
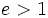 .
.
- Como la hipotenusa del triángulo rectángulo es mayor que los catetos, tenemos que
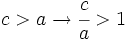
|
Actividad interactiva: Excentricidad de la hipérbola
Actividad 1: En la siguiente escena vamos a ver como se ve afectada la hipérbola si modificamos su excentricidad.
Actividad: Ejercicios: Modifica el valor de e (deslizando el punto verde) y observa los cambios.
Pulsa el botón Actualizar para recuperar la imagen inicial. Modifica el valor de a y observa los cambios.
|
Ecuaciones de la elipse
Ecuación reducida de la elipse
Ecuación reducida de la elipse
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de abscisas es:
, con centro en el origen de coordenadas y focos en el eje de abscisas es:
|
|
Sean  y
y  los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
los focos de la elipse. Cualquier punto P(x,y) de la misma cumple:
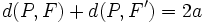
Sustituyendo las distancias por su fórmula matemática:
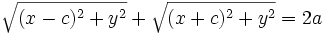
Pasamos la segunda raíz al segundo miembro:
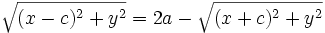
Se elevan al cuadrado ambos miebros y se simplifica:
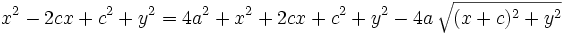
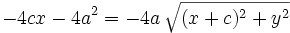
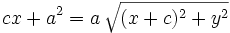
Se elevan al cuadrado los dos miembros:
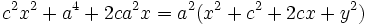
Reordenando y agrupando términos:
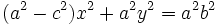
Teniendo en cuenta que 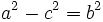 :
:
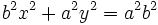
Dividiendo la expresión por 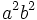 :
:
se obtiene la cuación buscada:
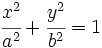
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación reducida de la elipse de semiejes 5 y 9.
Actividad: La ecuación reducida viene dada por la fórmula: 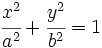 Sustituyendo a=5 y b=3, tenemos: 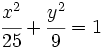 Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Ecuación de la elipse con los focos en el eje Y
Ecuación de la elipse con los focos en el eje Y
- La ecuación de una elipse con semieje mayor
 y semieje menor
y semieje menor  , con centro en el origen de coordenadas y focos en el eje de ordenadas es:
, con centro en el origen de coordenadas y focos en el eje de ordenadas es:
|
|
- Su excentricidad es:

Ecuación de la elipse con el centro desplazado del origen de coordenadas
Ecuación de la elipse con el centro desplazado del origen
- La ecuación de una elipse con semiejes
 y
y  y centro
y centro 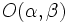 es:
es:
|
|
|
Actividad interactiva: Ecuación reducida de la elipse
Actividad 1: En la siguiente escena vamos a calcular la ecuación de la elipse de centro O(3,-1) y semiejes 5 y 2.
Actividad: La ecuación reducida viene dada por la fórmula: 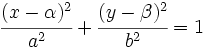 Sustituyendo  Puedes ver su gráfica en la siguente escena: Ejercicio:
|
Construcciones de la elipse
|
Actividad interactiva: Construcciones de la elipse
Actividad 1: Método del jardinero.
Actividad: Los jardineros, para trazar una forma elíptica sobre la tierra, clavan dos estacas en el suelo, atan entre ambas una cuerda suficientemente amplia y, manteniéndola tensa, trazan una línea sobre la tierra apoyando un palo sobre la cuerda y deslizándolo sobre la misma. En la siguiente escena, activa la traza, desliza el punto P y observa.
Actividad 2: La elipse como envolvente (1).
Actividad: Desliza el punto Q y observa.
Activa el trazo de QR y vuelve a deslizar el punto Q
Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior.
Actividad 3: La elipse como envolvente (2).
Actividad: Desliza el punto Q y observa. La figura muestra por donde habría de doblarse la cicunferencia (si fuese de papel) para que el punto Q coincidiese con el F. Activa el trazo de la cuerda y vuelve a deslizar el punto Q
Tras pulsar sobre para volver a la figura inicial, modifica la posición de F y repite lo anterior.
Actividad 4: La elipse a partir de dos circunferencias.
Actividad: Desliza el punto Q y observa.
Actividad 5: La elipse como hipotrocoide.
Actividad 6: La elipse mediante el compás de Arquímedes.
Actividad: Al utilizar el deslizador comprobarás el movimiento de un segmento de longitud fija cuyos extremos se deslizan sobre dos ejes perpendiculares.
Actividad 7: La elipse a partir de dos circunferencias tangentes interiores.
Actividad: Desliza el punto Q y observa. Activa el trazo del centro de la circunferencia interior y vuelve a deslizar el punto Q. |
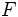 y
y 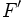 , con asíntotas
, con asíntotas  y
y 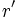 , con ejes de simetría
, con ejes de simetría 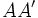 y su perpendicular pasando por su centro
y su perpendicular pasando por su centro  , determina los siguientes segmentos:
, determina los siguientes segmentos:
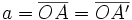
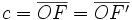
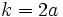 (constante de la hipérbola)
(constante de la hipérbola)
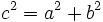

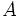 un punto de la hipérbola:
un punto de la hipérbola:
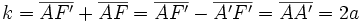
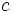 , tenemos
, tenemos

 ,
, 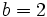 ,
, 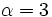 ,
,  , tenemos:
, tenemos: