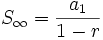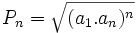Plantilla:Progresiones geométricas

De Wikipedia

(Diferencia entre revisiones)

Revisión de 09:54 14 ago 2016

Tabla de contenidos

1 Progresiones geométricas

Progresiones geométricas

Una progresión geométrica es una sucesión de números en la que cada término se obtiene multiplicando el anterior por una cantidad fija, $r\;\!$ , que llamaremos razón

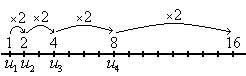
Por ejemplo:

es una progresión geométrica de razón r=2.

Término general de una progresión geométrica

Término general de una progresión geométrica

Sean 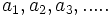$a_1, a_2, a_3, ..... \;\!$ términos de una progresión geométrica de razón $r\;\!$ .

Entonces se cumple que:

$a_n = a_1 \cdot r^{n-1}$

Demostración:

En efecto, de forma intuitiva:

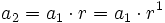
$a_2 = a_1 \cdot r = a_1 \cdot r^1 \;\!$

$a_3 = a_2 \cdot r = a_1 \cdot r \cdot r = a_1 \cdot r^2 \;\!$

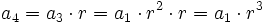
$a_4 = a_3 \cdot r = a_1 \cdot r^2 \cdot r = a_1 \cdot r^3 \;\!$

........................

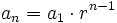
$a_n = a_1 \cdot r^{n-1}$

Demostración por el método de inducción completa:

Para ello hay que comprobar primero que la fórmula se cumple para n=1. A continuación, suponiendo que la fórmula es cierta para el valor n, deberemos comprobar que también se cumple para el valor n+1. Con ésto, la fórmula será cierta para todo valor n natural.

Veamos que se cumple para n=1. Sustituimos n por 1 en el lado derecho de la fórmula:

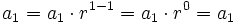
$a_1 = a_1 \cdot r^{1-1} = a_1 \cdot r^0 = a_1$

con lo que queda comprobada para n=1.

Supongamos que la fórmula es cierta para el valor n. Debemos comprobar que se cumple para el valor n+1.

Sustituimos n por n+1 en el lado derecho de la fórmula:

$a_1 \cdot r^{n+1-1}= a_1 \cdot r^n$ [1]

Por otro lado sabemos que 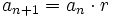$a_{n+1}=a_n \cdot r \;$ , y como hemos supuesto que la igualdad es cierta para el valor n, 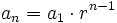$a_n = a_1 \cdot r^{n-1}$ , tenemos que:

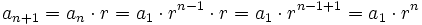
$a_{n+1}=a_n \cdot r = a_1 \cdot r^{n-1} \cdot r = a_1 \cdot r^{n-1+1} = a_1 \cdot r^n\;$

con lo que llegamos a la misma expresión que en [1], verificando así que la fórmula se cumple para el valor n+1 y terminando la demostración por inducción.

Suma de términos de una progresión geométrica

Suma de términos de una progresión geométrica

La suma de los n primeros términos de una progresión geométrica es:

$S_n=\frac{a_1.r^n-a_1}{r-1}$

Demostración:

Efectuamos la siguiente resta:

$r \cdot S_n \qquad ~= \qquad \quad a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n +a_n \cdot r$

$-\;$

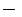
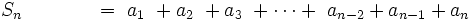
$S_n \ \qquad ~~~~= \ a_1 \ + a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n$

______________________________________________________________________________

$r \cdot S_n- S_n= -a_1 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ~~+a_n \cdot r$

por tanto:

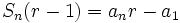
$S_n(r-1)=a_n r-a_1\;$

y despejando

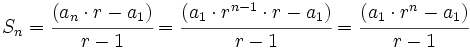
$S_n=\cfrac{(a_n \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^{n-1} \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^n - a_1)}{r-1}$

Suma de n términos consecutivos de una progresión geométrica (6´48") Sinopsis:

Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica

Suma de los infinitos términos de una progresión geométrica

La suma de todos los términos de una progresión geométrica en la que su razón verifica que 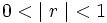$0<\; \mid r \mid \; <1$ se obtiene así:

$S_{\infty}=\frac{a_1}{1-r}$

Demostración:

La siguiente demostración usa el concepto de límite que aún no conoceis. Lo podremos ver con detalle, más adelante en este tema, en un apartado titulado Algunos límites importantes.

Vamos a partir de la fórmula de la suma de los n primeros términos de una progresión geométrica y vamos a hacer que n tienda a infinito.

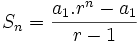
$S_n=\frac{a_1.r^n-a_1}{r-1}$

Como 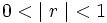$0<\; \mid r \mid \; <1$ , cuando n tiende a infinito, 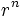$r^n\;$ tiende a 0.

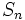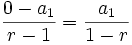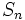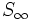Entonces, $S_n\;$ tiende a $\frac{0-a_1}{r-1}=\frac{a_1}{1-r}$ y a ese valor límite de $S_n\;$ lo llamamos $S_{\infty}$ .

Producto de términos de una progresión geométrica

Producto de n términos de una progresión geométrica

El producto de los n primeros términos de una progresión geométrica es:

$P_n=\sqrt{(a_1.a_n)^n}$

Demostración:

Véase en el siguiente videotutorial:

Producto de n términos de una progresión geométrica (7´31") Sinopsis:

Demostración de la fórmula del producto de n términos de una progresión geométrica

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Progresiones_geom%C3%A9tricas"

 <center><math>S_n=\cfrac{(a_n \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^{n-1} \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^n - a_1)}{r-1}</math></center>
+}}
+{{p}}
+{{Video_enlace
+|titulo1=Suma de n términos consecutivos de una progresión geométrica
+|duracion=6´48"
+|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/07-suma-de-terminos-consecutivos-de-una-sucesion-geometrica#.VCaqh_l_u2E
+|sinopsis=Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica
 }}
 {{p}}
 Entonces, <math>S_n\;</math> tiende a <math>\frac{0-a_1}{r-1}=\frac{a_1}{1-r}</math> y a ese valor límite de <math>S_n\;</math> lo llamamos <math>S_{\infty}</math>.
-}}
-{{p}}
-{{Video_enlace
-|titulo1=Suma de n términos consecutivos de una progresión geométrica
-|duracion=6´48"
-|url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/07-suma-de-terminos-consecutivos-de-una-sucesion-geometrica#.VCaqh_l_u2E
-|sinopsis=Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica
 }}

Plantilla:Progresiones geométricas

De Wikipedia

Revisión de 09:54 14 ago 2016

Tabla de contenidos

Progresiones geométricas

Término general de una progresión geométrica

Suma de términos de una progresión geométrica

Producto de términos de una progresión geométrica

Vistas

Herramientas personales

Menú

Buscar

Herramientas