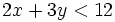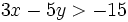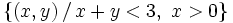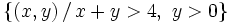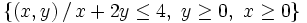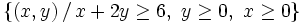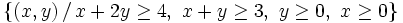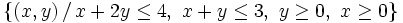Inecuaciones lineales con dos incógnitas (1ºBach)
De Wikipedia
| Revisión de 10:42 4 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:19 4 sep 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 76: | Línea 76: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | ==Sistemas de inecuaciones lineales con dos incógnitas== | ||
| + | {{Caja Amarilla|texto=*Un '''sistema de inecuaciones lineales con dos incógnitas''' es un conjunto de inecuaciones lineales con una incógnita. | ||
| + | * Una '''solución''' de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.}} | ||
| + | {{p}} | ||
| + | ==Resolución de un sistema de inecuaciones lineales con dos incógnitas== | ||
| + | Para averiguar las soluciones de un sistema de este tipo, recurriremos al método gráfico, igual que se hace con una sola inecuación. | ||
| + | La solución del sistema será la intersección de los semiplanos solución de cada una de las inecuaciones. | ||
| + | |||
| [[Categoría: Matemáticas]][[Categoría: Álgebra]] | [[Categoría: Matemáticas]][[Categoría: Álgebra]] | ||
Revisión de 19:19 4 sep 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Inecuación lineal con dos incógnitas
Una inecuación lineal con dos incógnitas es una inecuación, en la que las expresiones algebaricas que intervienen en la desigualdad, son polinomios de primer grado con dos variables. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
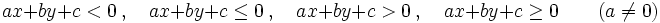
donde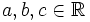 
son los coeficientes y 
e 
son las dos variables.
Soluciones de una inecuación lineal con dos incógnitas
Para resolver estas inecuaciones recurriremos a un método gráfico.
Resolución de las inecuaciones lineales con dos incógnitas
Las soluciones de una inecuación lineal con dos incógnitas son los puntos de uno de los dos semiplanos que se encuentran a cada lado de la recta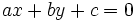 
.
Los puntos de uno de los semiplanos cumplen la condición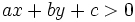 
y los del otro, la condición 
.
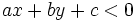Así, para determinar el semiplano solución, se elige un punto de cualquiera de ellos, y se comprueba si cumple la inecuación. Si la cumple, el semiplano que contiene al punto elegido es la solución, y si no, lo es el otro.
Si la inecuación no es estricta, los puntos de la recta también son solución, ya que para ellos se verifica la igualdad.
Ejercicio resuelto: Inecuaciones lineales con dos incógnitas
- 1. Resuelve la siguiente inecuación:
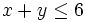
Solución 1 Descripción: En esta escena de Geogebra podrás ver como se representa gráficamente las soluciones de la inecuación .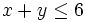
Videotutoriales
Inecuaciones lineales con dos incógnitas (6´55") Sinopsis: - Definición de inecuación.
- Ejemplos de inecuaciones lineales con dos incógnitas.
2 ejercicios (12´49") Sinopsis: Representa gráficamente las siguientes inecuaciones:
4 ejercicios (12´31") Sinopsis: Representa gráficamente los siguientes conjuntos:
2 ejercicios (4´59") Sinopsis: Representa gráficamente los siguientes conjuntos:
Sistemas de inecuaciones lineales con dos incógnitas
- Un sistema de inecuaciones lineales con dos incógnitas es un conjunto de inecuaciones lineales con una incógnita.
- Una solución de este tipo de sistemas es un punto del plano que satisface todas las inecuaciones simultaneamente.
Resolución de un sistema de inecuaciones lineales con dos incógnitas
Para averiguar las soluciones de un sistema de este tipo, recurriremos al método gráfico, igual que se hace con una sola inecuación. La solución del sistema será la intersección de los semiplanos solución de cada una de las inecuaciones.
