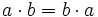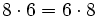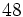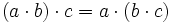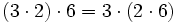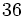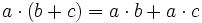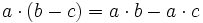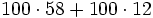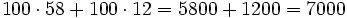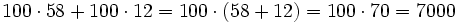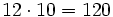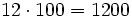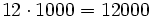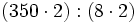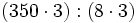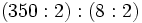Operaciones con números naturales (1º ESO)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 13:50 6 sep 2016

Menú:

Enlaces internos	Para repasar	Para ampliar	Enlaces externos
Indice Descartes Manual Casio			WIRIS Geogebra Calculadora

Tabla de contenidos

1 Suma y resta
2 Propiedades de la suma
3 Uso del Paréntesis
4 Multiplicación o producto
5 Propiedades de la multiplicación
- 5.1 La distributiva del producto
- 5.2 Producto por 10, 100, 1000, ....
6 División
- 6.1 Cociente por defecto y por exceso
- 6.2 Propiedades de la división
7 Orden en el que han de hacerse las operaciones

Suma y resta

Sumar es unir, juntar, añadir.
Restar es quitar, hallar lo que falta o lo que sobra es decir , calcular la diferencia.

Propiedades de la suma

Propiedades de la suma

Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.

$a+b = b+a\,$

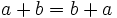
Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.

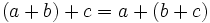
$(a + b ) + c = a + ( b + c )\,$

Ejemplo:

Conmutativa:

$8 + 6 = 6 + 8\,$

$14 = 14\,$

Asociativa:

$( 3 + 2 ) + 6 = 3 + ( 2 + 6 )\,$

$5 + 6 = 3 + 8\,$

$11 = 11\,$

$8 + 6 = 6 + 8\,$

$14\,$

   </div></td>

<td>

$(a + b ) + c = a + ( b + c )\,$

$11\,$

</td>

 </tr>

</table> </center>

Sumas Descripción:

Cálculo mental con sumas.

Restas Descripción:

Cálculo mental con restas.

Ejercicio: operaciones con la suma y la resta

1. Los gastos en €, de una familia durante los meses de abril y mayo han sido los siguientes

	Abril	Mayo
Alimentación	7589	8230
Vivienda	2567	2890
Gas	1045	856
Electricidad	724	689
Varios	1545	1835

a) ¿En cuál de los meses se ha gastado más?

b) ¿Qué apartado ha tenido mayor aumento de gasto de un mes a otro?

c) ¿En qué apartado se ha conseguidoel mayor ahorro de un mes a otro?

Solución:

a) Abril 13470 €; Mayo 14500 € b) Alimentación con 641 € más c) Gas con 189 € menos

Uso del Paréntesis

En las expresiones con operaciones combinadas, los paréntesis empaquetan resultados y modifican el orden en que han de realizarse las operaciones.

Ejemplo: Sumas y Restas con paréntesis y sin paréntesis

Jesús está mirando los últimos movimientos en su cuenta corriente. Tenía 2500 €; primero pago 450 € de gas, después pagó 325 € de luz y por último ingresó 1000 €.

¿Cuánto dinero le queda a Jesús en su cuenta?.

Solución:

Se puede hacer de dos formas:

a) 2500 - 450 - 325 + 1000 = 3500 - 775 = 2725

b) 2500 - ( 450 +325 )+ 1000 = 2500 -775 + 1000 = 2725

En ambos casos la solución es 2725 €.

Ejercicio: Sumas y restas con paréntesis

1. Calcula

a) 52 - (25 - 13)=

b) 40 - (32 - 16)=

c) 28 + (11 - 6)=

d) 37 + (15 - 12)=

Solución:

a) 40; b) 24; c) 33; d) 40

Multiplicación o producto

Multiplicar, es una forma abreviada de realizar una suma de sumandos iguales.

Ejemplo

Si un comerciante vende 5 equipos de sonido a 250 € cada uno, el dinero que ingresa es:

$250 + 250 + 250 + 250 + 250 = 250 \cdot 5 = 1250$ €

Actividad Interactiva: Multiplicación

Actividad 1: Cálculo mental con multiplicaciones.

Actividad:

Click aquí si no se ve bien la escena

Ejercicio: la multiplicación

1. Expresa como sumas de sumandos repetidos los siguientes productos

a) 3 . 5 =

b) 3 . 243 =

c) 7 . 5 =

Solución:

a) 3+3+3+3+3 ó 5+5+5 ; b) 3. 243 = 243 . 3 = 243 + 243 + 243; c) 7+7+7+7+7 ó 5+5+5+5+5+5+5;

Actividad Interactiva: Pregunta la tabla de multiplicar

Actividad 1: Asocia los factores con su producto

Actividad:

Click aquí si no se ve bien la escena

Propiedades de la multiplicación

Propiedad Conmutativa	Propiedad Asociativa
El producto no varía al cambiar el orden de los factores	El resultado de la multiplicación es independiente de la forma en que se agrupen los factores
$a \cdot b = b \cdot a$ $8 \cdot 6 = 6 \cdot 8$ $48\,$	$(a \cdot b ) \cdot c = a \cdot ( b \cdot c )$ $( 3 \cdot 2 ) \cdot 6 = 3 \cdot( 2 \cdot 6 )$ $36\,$

La distributiva del producto

El producto de un números por una suma (o resta ), es igual a la suma (o resta) de los productos parciales del número por cada sumando.

$a \cdot ( b + c ) = a \cdot b + a \cdot c$
$a \cdot ( b - c ) = a \cdot b - a \cdot c$

Ejemplo

Podemos calcular $100 \cdot 58 + 100 \cdot 12$ de dos formas distintas:

Primera forma:

$100 \cdot 58 + 100 \cdot 12 = 5800 + 1200 = 7000$

Segunda forma:

$100 \cdot 58 + 100 \cdot 12 = 100 \cdot (58 + 12) = 100 \cdot 70 = 7000$

Ejemplo: Propiedad distributiva del producto

Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?

Solución:

Podemos resolver el problema de dos formas:

Primera forma:

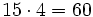
Alfredo-----> $15 \cdot 4 = 60$

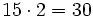
Teresa------> $15 \cdot 2 = 30$

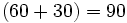Total---------> $(60 + 30)= 90\,$ €

Segunda forma:

Alfredo + Teresa compran 4 + 2 entradas

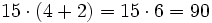Luego en total gastan entre los dos: $15 \cdot (4 + 2 )= 15 \cdot 6 = 90$ €

Actividad Interactiva: Propiedad Distributiva

Actividad 1: Asocia las expresiones numéricas equivalentes

Actividad:

Click aquí si no se ve bien la escena

Producto por 10, 100, 1000, ....

Para multiplicar un número por la unidad seguida de ceros (10. 100, 1000,...), se añaden a la derecha del número tantos ceros como acompañan a la unidad (uno, dos , tres,...).

Ejemplos

$12 \cdot 10 = 120$
$12 \cdot 100 = 1200$
$12 \cdot 1000 = 12000$

División

Dividir consiste en repartir en partes iguales o partir en partes de un determinado tamaño.

Una división puede ser exacta o entera dependiendo de su resto:

Si el resto es 0 la división es exacta y el dividendo es igual al divisor por cociente: $D = d.c\,$
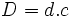
Si el resto es distinto de cero la división es entera y el dividendo es igual al divisor por cociente mas el resto: $D= d . c + r\,$

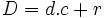
Actividad Interactiva: División

Actividad 1: Cálculo mental con divisiones.

Actividad:

Click aquí si no se ve bien la escena

Actividad 2: División entera.

Actividad:

Click aquí si no se ve bien la escena

Cociente por defecto y por exceso

Ejemplo: Cociente por defecto y por exceso

Un autobús con 40 turistas sufre una avería camino de la estación . Como no hay tiempo, pues el tren no espera, el responsable del grupo decide acomodar a los viajeros en taxis de 4 plazas.

a) ¿Cuántos taxis completarán?

b) Supongamos ahora que fuesen 43 turistas . ¿ Cuántos taxis completarían ?.

c) Y si nos preguntaran ¿cuántos taxis se necesitan?

d) ¿cuál es el cociente por defecto y por exceso?

Solución:

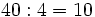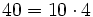a) $40 : 4 = 10\,$ ---> completarán 10 taxis. ( $40= 10 \cdot 4$ )
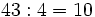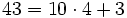b) $43 : 4 = 10\,$ y sobrarían 3 turistas. ( $43= 10 \cdot 4 + 3$ )
c) La respuesta sería 11, aunque en el último taxi quede un asiento libre.

d) El cociente por defecto sería 10 y el cociente por exceso sería 11.

Propiedades de la división

Alteraciones del cociente en una división

Exacta: Si el dividendo y el divisor de una división exacta se multiplica o se divide por un mismo número distinto de cero, el cociente no varía.
Entera: Si se multiplica o se divide el dividendo y el divisor por un mismo número distinto de cero, el cociente no varía pero el resto queda multiplicado o dividido por dicho número

Ejemplo: Propiedades de la división

Observa la siguiente división exacta , 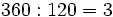$360 : 120 = 3\,$ , y escribe los cocientes de las siguientes divisiones sin hacerlas:

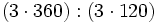
a) $(3 \cdot 360) : (3 \cdot 120)$

b) $36 : 12\,$

c) $18 : 6\,$

Solución:

a) 3; b) 3; c) 3.

Ejercicio: Propiedades de la división

Observa la siguiente división entera , 350: 8 = 43 y resto 6 , y calcula el cociente y el resto de las siguientes divisiones sin hacerlas:

a) $(350 \cdot 2) : (8 \cdot 2)$

b) $(350 \cdot 3) : (8 \cdot 3)$

c) $(350 : 2) : (8 : 2)\,$

Solución:

a) cociente=43 resto=12

b) cociente=43 resto=18

c) cociente=43 resto=3

Orden en el que han de hacerse las operaciones

En las expresiones con operaciones combinadas, hemos de atender:

1º a los paréntesis.
2º a las multiplicaciones y a las divisiones.
3º a las sumas y a las restas.

Ejercicio: Prioridad en las operaciones

2. Calcula utilizando el orden de operaciones

a) 4 . 6 + 2 . 8 - 3 . 4 =

b) 4 . (6 + 2) . 8 - 3 . 4 =

c) 4 . 6 + 2 . (8 - 3) . 4 =

d) 4 . 6 + (2 . 8 - 3) . 4 =

e) 4 . (6 + 2 . 8) - 3 . 4 =

f) 4 . (6 + 2 . 8 - 3) . 4 =

Solución:

a)28; b)244; c)64; d)76; e)76; f)304;

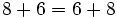
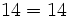
Obtenido de "http://maralboran.org/wikipedia/index.php/Operaciones_con_n%C3%BAmeros_naturales_%281%C2%BA_ESO%29"

Categorías: Matemáticas | Números

 {{Caja Amarilla|texto=*'''Sumar''' es unir, juntar, añadir.
 *'''Restar''' es quitar, hallar lo que falta o lo que sobra es decir , calcular la diferencia.
+}}
+{{p}}
+==Propiedades de la suma==
+{{Teorema_sin_demo|titulo=Propiedades de la suma|enunciado=
+*'''Propiedad conmutativa''': La suma no varía al cambiar el orden de los sumandos.{{p}}
+<center><math>a+b = b+a\,</math> </center>
+*'''Propiedad asociativa''': El resultado de la suma es independiente de la forma en que se agrupen los sumandos.{{p}}
+<center><math>(a + b ) + c = a + ( b + c )\,</math></center>
+}}
+{{p}}
+{{Ejemplo_simple|titulo=Ejemplo:|contenido=
+'''Conmutativa:'''
+<center><math>8 + 6 = 6 + 8\,</math></center>
+<center><math>14 = 14\,</math></center>
+'''Asociativa:'''
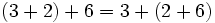
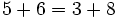
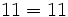
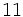
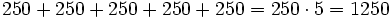+<center><math>( 3 + 2 ) + 6 = 3 + ( 2 + 6 )\,</math></center>
+<center><math>5 + 6 = 3 + 8\,</math></center>
+<center><math>11 = 11\,</math></center>
+      <p><strong><math>8 + 6 = 6 + 8\,</math> </strong></p>
+      <p><strong><math>14\,</math> </strong></p>
+    </div></td>
+    <td><div align="center">
+      <p><strong><math>(a + b ) + c = a + ( b + c )\,</math> </strong></p>
+      <p><strong></strong></p>
+      <p><strong><math>11\,</math></strong></p>
+    </div></td>
+  </tr>
+</table>
+</center>
 }}
 {{p}}
 }}
-==Propiedades de la suma==
-<center><table width="600" border="1">
-  <tr bgcolor="#CCCCCC">
-    <td width="282"><div align="center" class="Estilo5"><span class="Estilo3">Propiedad Conmutativa </span></div></td>
-    <td width="302"><div align="center" class="Estilo5"><span class="Estilo3">Propiedad Asociativa</span></div></td>
-  </tr>
-  <tr>
-    <td><div align="center"><span class="Estilo7">La suma no var&iacute;a al cambiar el orden de los sumandos </span></div></td>
-    <td><div align="center"><span class="Estilo7">El resultado de la suma es independiente de la forma en que se agrupen los sumandos </span></div></td>
-  </tr>
-  <tr>
-    <td><div align="center">
-      <p><strong><math>a+b = b+a\,</math> </strong></p>
-      <p><strong><math>8 + 6 = 6 + 8\,</math> </strong></p>
-      <p><strong><math>14\,</math> </strong></p>
-    </div></td>
-    <td><div align="center">
-      <p><strong><math>(a + b ) + c = a + ( b + c )\,</math> </strong></p>
-      <p><strong><math>( 3 + 2 ) + 6 = 3 + ( 2 + 6\,</math> )</strong></p>
-      <p><strong><math>11\,</math></strong></p>
-    </div></td>
-  </tr>
-</table>
-</center>
 ==Multiplicación o producto==

Operaciones con números naturales (1º ESO)

De Wikipedia

Revisión de 13:50 6 sep 2016

Tabla de contenidos

Suma y resta

Propiedades de la suma

Uso del Paréntesis

Multiplicación o producto

Propiedades de la multiplicación

La distributiva del producto

Producto por 10, 100, 1000, ....

División

Cociente por defecto y por exceso

Propiedades de la división

Orden en el que han de hacerse las operaciones

Vistas

Herramientas personales

Menú

Buscar

Herramientas