Plantilla:Ejemplo suma fracciones
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 14:02 18 sep 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:09 4 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 11: | Línea 11: | ||
| <center><math>=\cfrac{9+8-6}{12}=\cfrac{11}{12}</math></center> | <center><math>=\cfrac{9+8-6}{12}=\cfrac{11}{12}</math></center> | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplos 2: ''Fracciones homogeneas'' | ||
| + | |duracion=7'32" | ||
| + | |sinopsis=Suma y resta de fracciones con el mismo denominador. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=x3k-O_jtxoU | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplos 2: ''Fracciones heterogeneas'' | ||
| + | |duracion=7'26" | ||
| + | |sinopsis=Suma y resta de fracciones con distinto denominador. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=8sViQZCKC9g | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 3: ''Fracciones heterogeneas'' | ||
| + | |duracion=4'28" | ||
| + | |sinopsis=Suma y resta de fracciones con distinto denominador. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=7eCKIMYzfCg | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 4: ''Fracciones heterogeneas'' | ||
| + | |duracion=11'01" | ||
| + | |sinopsis=Suma y resta de fracciones con distinto denominador. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=I2F9Bbu89_E | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_julioprofe | ||
| + | |titulo1=Ejemplo 5: ''Números mixtos'' | ||
| + | |duracion=11'55" | ||
| + | |sinopsis=Suma y resta de números mixtos. | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=8vuByH9Ic28 | ||
| + | }} | ||
| + | {{p}} | ||
Revisión de 18:09 4 may 2017
Ejemplo: Suma y resta de fracciones
Calcula: 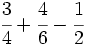
Solución:
Primero reducimos a común denominador. Para ello, calculamos el m.c.m. de los denominadores:
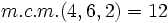 .
.
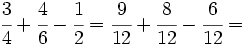
Luego sumamos o restamos los númeradores, dejando el mismo denominador:
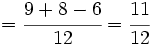
Suma y resta de fracciones con el mismo denominador.
Suma y resta de fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma y resta de fracciones con distinto denominador.
Suma y resta de números mixtos.

