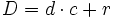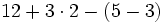Operaciones con números naturales (1º ESO)
De Wikipedia
| Revisión de 14:23 18 sep 2016 Coordinador (Discusión | contribuciones) (→Ejercicios propuestos) ← Ir a diferencia anterior |
Revisión de 14:24 18 sep 2016 Coordinador (Discusión | contribuciones) (→Operaciones combinadas) Ir a siguiente diferencia → |
||
| Línea 331: | Línea 331: | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplo:|contenido= | {{Ejemplo_simple|titulo=Ejemplo:|contenido= | ||
| - | :Efectúa las siguientes operaciones combinadas: <math>8+4 \cdot (5-2)</math> | + | Efectúa las siguientes operaciones combinadas: <math>8+4 \cdot (5-2)</math> |
| - | :'''Solución:''' | + | '''Solución:''' |
| # Los paréntesis <math>\rightarrow 8+4 \cdot (5-2)= 8 + 4 \cdot 3</math> | # Los paréntesis <math>\rightarrow 8+4 \cdot (5-2)= 8 + 4 \cdot 3</math> | ||
| # Las multiplicaciones y divisiones <math>\rightarrow 8 + 4 \cdot 3 = 8 + 12</math> | # Las multiplicaciones y divisiones <math>\rightarrow 8 + 4 \cdot 3 = 8 + 12</math> | ||
| Línea 344: | Línea 344: | ||
| |cuerpo= | |cuerpo= | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| - | |enunciado=:Calcula: | + | |enunciado=Calcula: |
| :a) <math>12+3 \cdot 2-(5-3)</math> | :a) <math>12+3 \cdot 2-(5-3)</math> | ||
| Línea 365: | Línea 365: | ||
| {{ejercicio_cuerpo | {{ejercicio_cuerpo | ||
| |enunciado= | |enunciado= | ||
| - | {{b4}}(Pág. 17) | + | (Pág. 17) |
| - | {{b4}}[[Imagen:red_star.png|12px]] 1a,b,c; 3a,c,e; 4a,c,e; 5, 6 | + | [[Imagen:red_star.png|12px]] 1a,b,c; 3a,c,e; 4a,c,e; 5, 6 |
| - | {{b4}}[[Imagen:yellow_star.png|12px]] 1d,e,f,g,h; 3b,d,f,g,h; 4b,d,f,g,h | + | [[Imagen:yellow_star.png|12px]] 1d,e,f,g,h; 3b,d,f,g,h; 4b,d,f,g,h |
| |sol=Usa la calculadora o Wolfram-Alpha para comprobar las soluciones: | |sol=Usa la calculadora o Wolfram-Alpha para comprobar las soluciones: | ||
Revisión de 14:24 18 sep 2016
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 12)
Suma y resta de números naturales
Suma
Sumar es unir, juntar, añadir.
Propiedades de la suma de números naturales
Propiedades de la suma
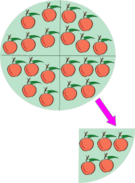
- Propiedad conmutativa: La suma no varía al cambiar el orden de los sumandos.
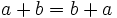
- Propiedad asociativa: El resultado de la suma es independiente de la forma en que se agrupen los sumandos.
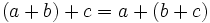
Cálculo mental con sumas.
Resta
Restar es quitar, hallar lo que falta o lo que sobra, es decir, calcular la diferencia.
Cálculo mental con restas.
Ejercicios propuestos
|
Ejercicios propuestos: Sumas y restas |
(Pág. 13)
Multiplicación o producto de números naturales
Multiplicar, es una forma abreviada de realizar una suma de sumandos iguales.
Cálculo mental con multiplicaciones.
Propiedades de la multiplicación de números naturales
Propiedades de la multiplicación
- Propiedad conmutativa: El producto no varía al cambiar el orden de los factores.
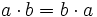
- Propiedad asociativa: El resultado de una multiplicación es independiente de la forma en que se agrupen los factores.
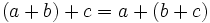
- Propiedad distributiva: El producto de un número por una suma (o resta) es igual a la suma (o rsta) de los productos del número por cada sumando.

Ejemplo: Propiedad distributiva del producto
Alfredo va a comprar cuatro entradas para un concierto de rock y Teresa va a comprar dos entradas . ¿ Cuánto pagarán entre los dos si cada entrada cuesta 15 €?
Podemos resolver el problema de dos formas:
- Primera forma:
- Alfredo----->
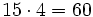
- Teresa------>
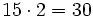
- Total--------->
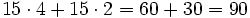 €
€
- Alfredo----->
- Segunda forma:
- Alfredo y Teresa compran 4 + 2 entradas
- Luego en total gastan entre los dos:
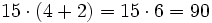 €
€
Asocia las expresiones numéricas equivalentes.
Producto por 10, 100, 1000, ....
Para multiplicar un número por la unidad seguida de ceros (10, 100, 1000,...), se añaden a la derecha del número tantos ceros como acompañan a la unidad (uno, dos , tres,...).
Ejercicios propuestos
|
Ejercicios propuestos: Multiplicación |
(Pág. 14-15)
División de números naturales
Dividir consiste en repartir una cantidad en partes iguales o partir en partes de un determinado tamaño. Mas concretamente:
Sean
|
Algoritmo de la división
Dados  y
y  , dos números naturales cualesquiera, existen dos únicos números naturales,
, dos números naturales cualesquiera, existen dos únicos números naturales,  y
y  , tales que:
, tales que:
|
|
 es el dividendo,
es el dividendo,  el divisor,
el divisor,  el cociente y
el cociente y  el resto.
el resto.
Ver demostración en Wikipedia
Cálculo con divisiones.
|
Actividad: Cociente y resto Calcula:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Cociente por defecto y por exceso
Ejemplo: Cociente por defecto y por exceso
Un autobús con 43 turistas sufre una avería camino de la estación . Como no hay tiempo, pues el tren no espera, el responsable del grupo decide acomodar a los viajeros en taxis de 4 plazas.
- a) ¿Cuántos taxis completarán?
- b) ¿Cuántos taxis se necesitan?
- c) ¿cuál es el cociente por defecto y por exceso?
a) Completan 10 taxis y sobran 3 turistas. (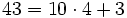 )
)
b) Se necesitan 11 taxis, aunque en el último taxi quede un asiento libre.
Propiedades de la división de números naturales
Propiedades
- La división de de números naturales no siempre es un número natural
- La división no tiene las mismas propiedades que producto. No tiene la propiedad conmutativa, ni la asociativa, ni la distributiva.
- Si se multiplica o se divide el dividendo y el divisor por un mismo número distinto de cero, el cociente no varía pero el resto queda multiplicado o dividido por dicho número.
Hagamos la división 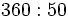
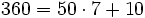 (Cociente=7; Resto=10)
(Cociente=7; Resto=10)Ahora dividimos el dividendo y el divisor por 10:
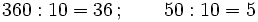
y volvemos a hacer la división:
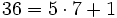 (Cociente=7; Resto=1)
(Cociente=7; Resto=1)Es decir, el cociente no varía y el resto queda dividido por 10.
Ejercicios propuestos
|
Ejercicios propuestos: División |
(Pág. 16-17)
Operaciones combinadas
Jerarquía de las operaciones
- Primero se efectúan las operaciones del interior de los paréntesis. Si hay paréntesis anidados, se efectúan de dentro hacia fuera.
- Dentro de los paréntesis, o una vez quitados todos los paréntesis, las operaciones se efectúan en el siguiente orden:
- Las multiplicaciones y las divisiones.
- Las sumas y las restas.
- Cuando aparecen paréntesis dentro de otros paréntesis, se puede optar por cambiar los paréntesis más exteriores por corchetes, con el fin de facilitar la lectura de la operación.
- Cuando resuelvas los paréntesis puedes completar las operaciones que encierren o aplicar la propiedad distributiva.
- En cada uno de los pasos que des para resolver una expresión con operaciones combinadas se puede llevar a cabo más de una operación, siempre que no suponga romper el orden que acabamos de establecer.
- No se incluyen las potencias ni las raíces en este esquema, pues estas operaciones se veran en otro tema. Lo que haremos será resolverlas después de resolver los paréntesis, antes de las multiplicaciones y divisiones.
Efectúa las siguientes operaciones combinadas: 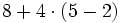
Solución:
- Los paréntesis
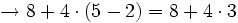
- Las multiplicaciones y divisiones
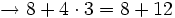
- Las sumas y restas
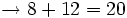
Ejercicios propuestos
|
Ejercicios propuestos: División |
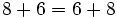
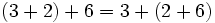
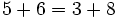
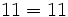
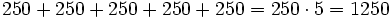 €
€
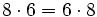
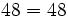
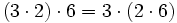

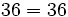
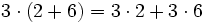
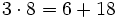
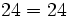
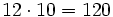
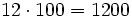
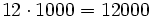
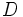 y
y 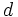 dos números naturales, con
dos números naturales, con 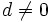 .
.
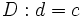
 , cociente.
, cociente.
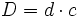 ), diremos que la división es exacta.
), diremos que la división es exacta.
 , menor que
, menor que 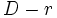 entre
entre