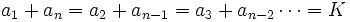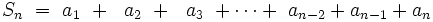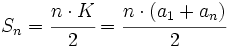Plantilla:Suma de términos de una progresión aritmética
De Wikipedia
| Revisión de 09:37 3 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:14 25 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 34: | Línea 34: | ||
| ::<math>S_n=\cfrac{n \cdot K}{2}=\cfrac{n \cdot (a_1+a_n)}{2}</math> | ::<math>S_n=\cfrac{n \cdot K}{2}=\cfrac{n \cdot (a_1+a_n)}{2}</math> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
| + | |descripcion=Suma los n primeros términos de una progresión aritmética dada. | ||
| + | |enlace=[https://ggbm.at/mCUgtBC4 Autoevaluación: Suma de términos de una progresión aritmética] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:14 25 nov 2016
Suma de términos de una progresión aritmética
La suma de los n primeros términos de una progresión aritmética es:
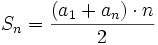
El porqué de esta fórmula se deduce de la siguiente historia:
En un pequeño pueblo de Alemania, Brunswick, un día en la escuela el profesor manda sumar los cien primeros números naturales. El maestro quería unos minutos de tranquilidad... pero transcurridos pocos segundos uno de los alumnos levanta la mano y dice tener la solución: los cien primeros números naturales suman 5.050. Y efectivamente, así era.
El profesor le preguntó ¿cómo lo has hecho? El niño le dijo: 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101,... siempre suma 101 y hay 50 sumas, en total 50 * 101 = 5050. El profesor quedó tan impresionado que le regaló un libro de Aritmética.
Ese niño tenía 10 años y se llamaba Carl Friedrich Gaüss. Fue uno de los mas grandes matemáticos. Intenta enterarte de algo más sobre él.
Demostración:
Para la demostración nos basaremos en el hecho de que:
Entonces, si efectuamos la siguiente suma:
- _______________________________________________________________
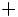
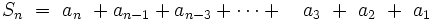
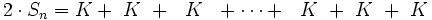
por tanto:
Suma los n primeros términos de una progresión aritmética dada.
Suma de los n primeros términos de una progresión aritmética (8´47") Sinopsis:Demostración de la fórmula de la suma de los n primeros términos de una progresión aritmética
