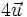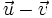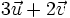Vectores: Coordenadas (1ºBach)
De Wikipedia
| Revisión de 19:14 7 oct 2016 Coordinador (Discusión | contribuciones) (→Coordenadas de un vector respecto de una base) ← Ir a diferencia anterior |
Revisión de 10:49 8 oct 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 7: | Línea 7: | ||
| {{p}} | {{p}} | ||
| ==Base de vectores en el plano== | ==Base de vectores en el plano== | ||
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=*Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, se puede poner como combinación lineal de ellos: | + | {{Teorema_sin_demo|titulo=Proposición|enunciado=*Dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}}, se puede poner como combinación lineal de ellos: |
| {{p}} | {{p}} | ||
| - | <center><math>\overrightarrow{v}=a \overrightarrow{x}+b \overrightarrow{x}</math></center> | + | <center><math>\vec{v}=a \vec{x}+b \vec{x}</math></center> |
| {{p}} | {{p}} | ||
| *Esta combinación lineal es única, es decir, sólo existen dos números <math>a\,</math> y <math>b\,</math> para los que se cumple la igualdad anterior. | *Esta combinación lineal es única, es decir, sólo existen dos números <math>a\,</math> y <math>b\,</math> para los que se cumple la igualdad anterior. | ||
| Línea 16: | Línea 16: | ||
| Estos resultados permiten dar la siguiente definición: | Estos resultados permiten dar la siguiente definición: | ||
| {{p}} | {{p}} | ||
| - | {{Caja_Amarilla|texto=Se llama '''base''' de un conjunto de vectores del plano a dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones. La representaremos por {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. | + | {{Caja_Amarilla|texto=Se llama '''base''' de un conjunto de vectores del plano a dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones. La representaremos por {{sube|porcentaje=+10%|contenido=<math>B(\vec{x},\vec{y})</math>}}. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 30: | Línea 30: | ||
| ==Coordenadas de un vector respecto de una base== | ==Coordenadas de un vector respecto de una base== | ||
| - | {{Caja_Amarilla|texto=Dada una base del plano {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}, por el teorema de la base, sabemos que cualquier vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} se puede poner como combinación lineal de los vectores de dicha base, de forma única: <math>\overrightarrow{v}=a \overrightarrow{x}+b \overrightarrow{x}</math> | + | {{Caja_Amarilla|texto=Dada una base del plano {{sube|porcentaje=+10%|contenido=<math>B(\vec{x},\vec{y})</math>}}, por el teorema de la base, sabemos que cualquier vector {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}} se puede poner como combinación lineal de los vectores de dicha base, de forma única: <math>\vec{v}=a \vec{x}+b \vec{x}</math> |
| - | *Al par de números <math>(a,b)\,</math> los llamaremos las '''coordenadas''' del vector {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\overrightarrow{x},\overrightarrow{y})</math>}}. Lo expresaremos {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{v}=(a,b)</math>}}, o bien, {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{v}(a,b)</math>}}. | + | *Al par de números <math>(a,b)\,</math> los llamaremos las '''coordenadas''' del vector {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}} respecto de la base {{sube|porcentaje=+10%|contenido=<math>B(\vec{x},\vec{y})</math>}}. Lo expresaremos {{sube|porcentaje=+10%|contenido=<math>\vec{v}=(a,b)</math>}}, o bien, {{sube|porcentaje=+10%|contenido=<math>\vec{v}(a,b)</math>}}. |
| - | *Las coordenadas de los vectores de la base son {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{x}(1,0)</math>}} e {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{y}(0,1)</math>}}, ya que {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{x}=1 \overrightarrow{x}+0 \overrightarrow{y}</math>}} y {{sube|porcentaje=+10%|contenido=<math>\overrightarrow{y}=0 \overrightarrow{x}+1 \overrightarrow{y}</math>}}. | + | *Las coordenadas de los vectores de la base son {{sube|porcentaje=+10%|contenido=<math>\vec{x}(1,0)</math>}} e {{sube|porcentaje=+10%|contenido=<math>\vec{y}(0,1)</math>}}, ya que {{sube|porcentaje=+10%|contenido=<math>\vec{x}=1 \vec{x}+0 \vec{y}</math>}} y {{sube|porcentaje=+10%|contenido=<math>\vec{y}=0 \vec{x}+1 \vec{y}</math>}}. |
| }} | }} | ||
| {{p}} | {{p}} | ||
| Línea 50: | Línea 50: | ||
| |duracion=13´40" | |duracion=13´40" | ||
| |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/08-vectores-en-el-plano/0802-dos-ejercicios-4#.VC2a0xa7ZV8 | |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/08-vectores-en-el-plano/0802-dos-ejercicios-4#.VC2a0xa7ZV8 | ||
| - | |sinopsis=*Demostración de que dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\overrightarrow{v}</math>}}, se puede poner como combinación lineal de ellos. | + | |sinopsis=*Demostración de que dados dos vectores {{sube|porcentaje=+30%|contenido=<math>\vec{x}</math>}} e {{sube|porcentaje=+30%|contenido=<math>\vec{y}</math>}}, con distintas direcciones, cualquier vector del plano, {{sube|porcentaje=+30%|contenido=<math>\vec{v}</math>}}, se puede poner como combinación lineal de ellos. |
| *Ejercicio: Si <math>\vec{u}=(2,1)</math>, <math>\vec{v}(3,-4)</math> y <math>\vec{z}=(1,6)</math>, expresa <math>\vec{z}</math> como combinación lineal de los otros dos vectores. | *Ejercicio: Si <math>\vec{u}=(2,1)</math>, <math>\vec{v}(3,-4)</math> y <math>\vec{z}=(1,6)</math>, expresa <math>\vec{z}</math> como combinación lineal de los otros dos vectores. | ||
| }} | }} | ||
| Línea 57: | Línea 57: | ||
| ==Operaciones con vectores dados por coordenadas== | ==Operaciones con vectores dados por coordenadas== | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| - | Sean {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{u}=(x_1,y_1)</math>}} y {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{v}=(x_2,y_2)</math>}} dos vectores del plano: | + | Sean {{sube|porcentaje=+25%|contenido=<math>\vec{u}=(x_1,y_1)</math>}} y {{sube|porcentaje=+25%|contenido=<math>\vec{v}=(x_2,y_2)</math>}} dos vectores del plano: |
| - | *'''Suma de vectores:''' {{sube|porcentaje=+25%|contenido=<math>\overrightarrow{u}+\overrightarrow{v}=(x_1+x_2,y_1+y_2)</math>}} | + | *'''Suma de vectores:''' {{sube|porcentaje=+25%|contenido=<math>\vec{u}+\vec{v}=(x_1+x_2,y_1+y_2)</math>}} |
| - | *'''Producto por un número k:''' {{sube|porcentaje=+25%|contenido=<math>k \overrightarrow{u}=(k \, x_1,k \, y_1)</math>}} | + | *'''Producto por un número k:''' {{sube|porcentaje=+25%|contenido=<math>k \vec{u}=(k \, x_1,k \, y_1)</math>}} |
| - | *'''Combinación lineal:''' {{sube|porcentaje=+25%|contenido=<math>a \overrightarrow{u}+b \overrightarrow{v}=(a \, x_1+ b \, x_2, a \, y_1+b \, y_2)</math>}} | + | *'''Combinación lineal:''' {{sube|porcentaje=+25%|contenido=<math>a \vec{u}+b \vec{v}=(a \, x_1+ b \, x_2, a \, y_1+b \, y_2)</math>}} |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 10:49 8 oct 2016
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadoras |
Tabla de contenidos |
Base de vectores en el plano
Proposición
- Dados dos vectores
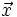 e
e 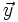 , con distintas direcciones, cualquier vector del plano,
, con distintas direcciones, cualquier vector del plano, 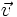 , se puede poner como combinación lineal de ellos:
, se puede poner como combinación lineal de ellos:
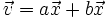
- Esta combinación lineal es única, es decir, sólo existen dos números
 y
y  para los que se cumple la igualdad anterior.
para los que se cumple la igualdad anterior.
Estos resultados permiten dar la siguiente definición:
Se llama base de un conjunto de vectores del plano a dos vectores 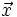 e
e 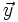 , con distintas direcciones. La representaremos por
, con distintas direcciones. La representaremos por 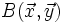 .
.
De esta manera, los resultados anteriores se pueden reenunciar de la siguiente manera:
Teorema de la base
Cualquier vector del plano se puede poner como combinación lineal de los vectores de una base, de forma única.
Base ortogonal y ortonormal
Si los dos vectores de una base del plano son perpendiculares entre sí, se dice que forman una base ortogonal. Si además ambos tienen módulo 1, se dice que forman una base ortonormal
Coordenadas de un vector respecto de una base
Dada una base del plano 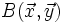 , por el teorema de la base, sabemos que cualquier vector
, por el teorema de la base, sabemos que cualquier vector 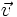 se puede poner como combinación lineal de los vectores de dicha base, de forma única:
se puede poner como combinación lineal de los vectores de dicha base, de forma única: 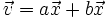
- Al par de números
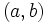 los llamaremos las coordenadas del vector
los llamaremos las coordenadas del vector 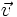 respecto de la base
respecto de la base 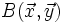 . Lo expresaremos
. Lo expresaremos 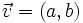 , o bien,
, o bien, 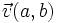 .
.
- Las coordenadas de los vectores de la base son
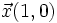 e
e 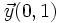 , ya que
, ya que 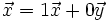 y
y 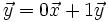 .
.
En esta escena podrás poner un vector como combinación lineal de los vectores de una base y obtener sus coordenadas respecto de ella.
Ejercicio de autoevaluación en el que podrás poner un vector como combinación lineal de otros dos no alineados y que, por tanto, constituyen una base de vectores del plano. En consecuncia podrás averiguar sus coordenadas respecto de dicha base, que serán los números por los que hay que multiplicar los vectores de la base para obtener el vector dado.
- Demostración de que dados dos vectores
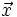 e
e 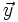 , con distintas direcciones, cualquier vector del plano,
, con distintas direcciones, cualquier vector del plano, 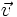 , se puede poner como combinación lineal de ellos.
, se puede poner como combinación lineal de ellos.
- Ejercicio: Si
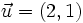 ,
, 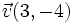 y
y 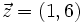 , expresa
, expresa 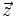 como combinación lineal de los otros dos vectores.
como combinación lineal de los otros dos vectores.
Operaciones con vectores dados por coordenadas
Sean 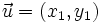 y
y 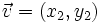 dos vectores del plano:
dos vectores del plano:
- Suma de vectores:
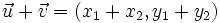
- Producto por un número k:
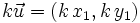
- Combinación lineal:
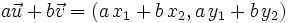
|
Actividad: Operaciones con vectores dados por coordenadas Sean
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones: a) vector 4(-2,1) b) vector (-2,1)-(1,2) c) vector 3(-2,1)+2(1,2) |
En esta escena podrás ver como se multiplica un vector por un número.
En esta escena podrás ver como se suman y restan vectores.
- Suma de vectores: método del paralelogramo.
- Coordenadas del vector suma.
- Propiedades de la suma de vectores.
- Producto de un escalar por un vector
- Propiedades
- Vectores colineales
Sean 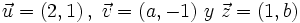 . Halla "a" y "b" en los siguientes casos:
. Halla "a" y "b" en los siguientes casos:
- a)
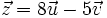
- b)
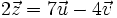
- c)
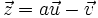
- d)
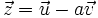
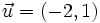 y
y 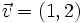 . Representa y halla las coordenadas de los siguientes vectores:
. Representa y halla las coordenadas de los siguientes vectores: