Plantilla:Sistemas equivalentes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 20:39 31 oct 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:15 1 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 3: | Línea 3: | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion='''Pincha en este enlace para realizar la siguiente actividad:''' | + | |descripcion=En esta escena podrás realizar la siguiente actividad en la que se comprueba como ciertas transformaciones hechas a un sistema dan lugar a otro sistema equivalente. |
| - | Dado el sistema: | + | Partirás del sistema: |
| <center><math>\left . \begin{matrix} 2x-y=6 \\ 3x+3y=18 \end{matrix} \right \}</math></center> | <center><math>\left . \begin{matrix} 2x-y=6 \\ 3x+3y=18 \end{matrix} \right \}</math></center> | ||
| - | :a) Represéntalo gráficamente y anota la solución. | + | y deberás contestar a las siguientes preguntas: |
| - | :b) Multiplica la primera ecuación por 3 y divide la segunda por 3. Representa el nuevo sistema. ¿Qué solución tiene el nuevo sistema?. ¿Es equivalente al sistema de partida? | + | #Este sistema está representado en la escena. ¿Cuál es su solución? |
| - | + | #Divide la segunda ecuación por 3, dejando la segunda ecuación igual. Representa el nuevo sistema. ¿Qué solución tiene el nuevo sistema?. ¿Es equivalente al sistema de partida? | |
| - | :c) Resta a la 2ª ecuación la 1ª ecuación y representa el sistema formado por esa nueva ecuación y una cualquiera de las dos ecuaciones del sistema de partida. ¿Qué solución tiene?. | + | #En el sistema obtenido en el apartado 2, suma la 2ª ecuación a la 1ª y representa el sistema formado por esa nueva ecuación y una cualquiera de las dos ecuaciones del sistema de partida (por ejemplo la segunda). ¿Qué solución tiene?. ¿Es equivalente al sistema de partida? |
| + | #En el sistema obtenido en el apartado 3, divide la primera ecuación (la que no tiene "y") por 3 y deja la segunda ecuación igual. ¿Qué solución tiene?. ¿Es equivalente al sistema de partida? | ||
| + | Podrás hacer uso de la escena para representar las ecuaciones de los sistemas que van a apareciendo en cada apartado. | ||
| |enlace=[https://ggbm.at/EuQne8v6 Actividad: Sistemas equivalentes] | |enlace=[https://ggbm.at/EuQne8v6 Actividad: Sistemas equivalentes] | ||
| }} | }} | ||
Revisión de 09:15 1 nov 2016
Dos sistemas son equivalentes cuando tienen las mismas soluciones.
En esta escena podrás realizar la siguiente actividad en la que se comprueba como ciertas transformaciones hechas a un sistema dan lugar a otro sistema equivalente.
Partirás del sistema:
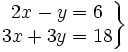
y deberás contestar a las siguientes preguntas:
- Este sistema está representado en la escena. ¿Cuál es su solución?
- Divide la segunda ecuación por 3, dejando la segunda ecuación igual. Representa el nuevo sistema. ¿Qué solución tiene el nuevo sistema?. ¿Es equivalente al sistema de partida?
- En el sistema obtenido en el apartado 2, suma la 2ª ecuación a la 1ª y representa el sistema formado por esa nueva ecuación y una cualquiera de las dos ecuaciones del sistema de partida (por ejemplo la segunda). ¿Qué solución tiene?. ¿Es equivalente al sistema de partida?
- En el sistema obtenido en el apartado 3, divide la primera ecuación (la que no tiene "y") por 3 y deja la segunda ecuación igual. ¿Qué solución tiene?. ¿Es equivalente al sistema de partida?
Podrás hacer uso de la escena para representar las ecuaciones de los sistemas que van a apareciendo en cada apartado.

