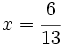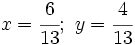Plantilla:Método de igualación
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:13 1 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:16 1 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 32: | Línea 32: | ||
| *Así, la solución del sistema es: | *Así, la solución del sistema es: | ||
| {{Caja|contenido=<math>x=\cfrac{6}{13}; \ y=\cfrac{4}{13}</math>}} | {{Caja|contenido=<math>x=\cfrac{6}{13}; \ y=\cfrac{4}{13}</math>}} | ||
| - | |||
| - | Comprueba en la siguiente escena la solución del sistema. para ello deberás introducir los coeficientes de cada ecuación en las casillas correspondientes. | ||
| - | |||
| - | <center><iframe> | ||
| - | url=http://maralboran.org/web_ma/descartes/Algebra/Sistemas_ecuaciones_lineales/sistema_1.html | ||
| - | width=450 | ||
| - | height=340 | ||
| - | name=myframe | ||
| - | </iframe></center> | ||
| - | <center>[http://maralboran.org/web_ma/descartes/Algebra/Sistemas_ecuaciones_lineales/sistema_1.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| }} | }} | ||
Revisión de 11:16 1 nov 2016
Procedimiento
El método de igualación consiste en despejar la misma incógnita en las dos ecuaciones e igualar las expresiones resultantes. Así, nos queda una ecuación con una sola incógnita. Esta se resuelve y permite averiguar dicha incógnita. Finalmente, el valor de la otra incógnita se obtiene sustituyendo el valor obtenido.
Ejemplo: Método de igualación
Resuelve por el método de igualación el siguiente sistema:
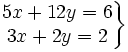
Solución:
- Despejamos la
en cada una de las dos ecuaciones:
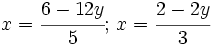
- Igualamos estas dos expresiones:
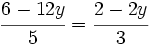
- Resolvemos la ecuación:
|
|
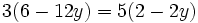
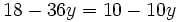
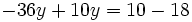
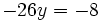
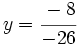
- Sustituimos el valor
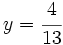en cualquiera de las expresiones del primer paso, por ejemplo en 
:
|
|
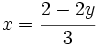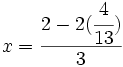
- Así, la solución del sistema es:
|
|
