Plantilla:Función afín
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:00 9 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 19:06 9 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | {{Caja_Amarilla|texto=Una '''función afín''' o '''lineal''' es aquella cuya expresión analítica es o puede ponerse como: | + | {{Caja_Amarilla|texto=Una '''función lineal''' es aquella cuya expresión analítica es o puede ponerse como: |
| {{caja|contenido=<center><math>y=mx+n\;</math></center>}} | {{caja|contenido=<center><math>y=mx+n\;</math></center>}} | ||
| Línea 6: | Línea 6: | ||
| *<math>m\;\!</math> es una constante que se denomina '''pendiente'''. | *<math>m\;\!</math> es una constante que se denomina '''pendiente'''. | ||
| *<math>n\;\!</math> es otra constante denominada '''ordenada en el origen'''. | *<math>n\;\!</math> es otra constante denominada '''ordenada en el origen'''. | ||
| + | |||
| + | Si n \ne 0 recibe el nombre de '''función afín'''. | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| - | |descripcion=En esta escena podrás ver e interactuar con las gráficas de funciones afines y estudiar sus propiedades. | + | |descripcion=En esta escena podrás ver e interactuar con las gráficas de funciones lineales y estudiar sus propiedades. |
| - | |enlace=[https://ggbm.at/QyCn33kQ Función afín] | + | |enlace=[https://ggbm.at/QyCn33kQ Función lineal] |
| }} | }} | ||
Revisión de 19:06 9 nov 2016
Una función lineal es aquella cuya expresión analítica es o puede ponerse como:
 |
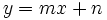e 
son variables.
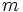es una constante que se denomina pendiente.
es otra constante denominada ordenada en el origen.
Si n \ne 0 recibe el nombre de función afín.
Función lineal Descripción: En esta escena podrás ver e interactuar con las gráficas de funciones lineales y estudiar sus propiedades.
