Plantilla:Perímetros y áreas
De Wikipedia
| Revisión de 18:16 15 nov 2016 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:17 15 nov 2016 Coordinador (Discusión | contribuciones) (→Rectángulo) Ir a siguiente diferencia → |
||
| Línea 91: | Línea 91: | ||
| {{widget generico}} | {{widget generico}} | ||
| }} | }} | ||
| - | + | }} | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 18:17 15 nov 2016
Tabla de contenidos |
Cuadrado

|
|
|
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del cuadrado; en la segunda podrás calcular el área y el perímetro del cuadrado.
|
Actividad: El cuadrado
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
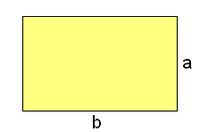
Rectángulo
|
|
|
En esta escena consta de dos partes: en la primera podrás deducir la fórmula del área del rectángulo; en la segunda podrás calcular el área y el perímetro del rectángulo.
|
Actividad: El rectángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Paralelogramo

|
|
|
|
Actividad interactiva: Paralelogramo
Actividad 1: Deducción de la fórmula del área del paralelogramo.
Actividad: El paralelogramo de la derecha tiene el mismo área que el rectángulo que tiene debajo. Para comprobarlo, mueve el punto que se indica y arrastralo hacia la izquierda. Por tanto el área del paralelogramo es el mismo que el del rectángulo. Deducción de la fórmula del área del paralelogramo
(Mueve el punto azul)
Actividad 2: La base de un paralelogramo es 5 cm, y su altura es 2,8 cm. ¿Cual es el área y el perímetro del paralelogramo?
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: Cálculo del área y del perímetro del paralelogramo
(Mueve los vértices para modificar la medida de los lados)
|
|
Actividad: Paralelogramo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
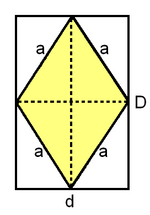
Rombo
|
|
|
|
Actividad interactiva: Rombo Actividad 1: Deducción del área del rombo. Actividad: Modifica el polígono arrastrando los puntos verdes
Actividad 2: La diagonal mayor de un rombo mide 5m, y la menor es la mitad. Calcula el área y el perímetro del rombo.
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: Cálculo del área y del perímetro del rombo
(Mueve los vértices para modificar la medida de los lados)
Actividad 3: Calcula el área de un cuadrado de 4 m. de diagonal.
Actividad: El cuadrado es un rombo que tiene las diagonales iguales. Para calcular el área del cuadrado puedes utilizar también la expresión del área del rombo. Comprueba en la figura que estas expresiones dan el mismo valor. El cuadrado es un rombo con los 4 lados iguales
(Mueve el vértice B para modificar la medida del lado)
|
|
Actividad: Rombo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
Triángulo
|
|
|
Actividad interactiva: Triángulo Actividad 1: Deducción del área del triángulo. Actividad: Desliza el punto verde o utiliza los botones, observa lo que ocurre y razona:
Vuelve a la posición inicial y modifica el triángulo arrastrando cualquiera de sus vértices. Vuelve a deslizar los puntos verdes.
Vuelve a la posición inicial y modifica el triángulo arrastrando cualquiera de sus vértices. Vuelve a deslizar el punto verde.
Actividad 2: La base de un triángulo isósceles mide 5 cm. y los lados iguales miden 3,7 cm. Halla su área y su perímetro.
Actividad: Hazlo en tu cuaderno y comprueba los resultados en la siguiente escena: El cuadrado es un rombo con los 4 lados iguales
(Mueve los vértices del triángulo para variar la medida de los lados)
|
Fórmula de Herón
La superficie de un triángulo de lados a, b, c viene dada por:
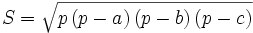
donde 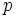 es el semiperímetro:
es el semiperímetro: 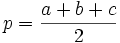 .
.
Nota: Esta demostración excede el nivel de este curso.
Una demostración moderna, que emplea álgebra y trigonometría (bastante distinta a la que dio Herón en su libro), podría ser la siguiente.
Supongamos un triángulo de lados a, b, c cuyos ángulos opuestos a cada uno de esos lados son A, B, C. Entonces tenemos que:
por el Teorema del coseno:
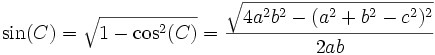 .
.
La altura de un triángulo de base a tiene una longitud bsin(C), por tanto siguiendo con la demostración
|
Actividad: Triángulo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
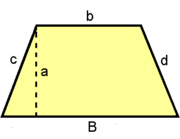
Trapecio
|
|
|
|
Actividad interactiva: Trapecio
1. Deducción de la fórmula del área de un trapecio.
Actividad: Para ello, mueve el punto rojo hacia la izquierda. Obtendrás un duplicado del trapecio en color azul, que junto con el trapecio amarillo inicial, forman un paralelogramo de base 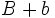 y altura y altura  . .
El área del paralelogramo es: 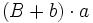 de donde, dividiendo por 2, obtenemos el área del trapecio: 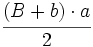 Deducción de la fórmula del área del trapecio
(Mueve el punto rojo)
2. Halla el área y el perímetro de un trapecio de base mayor 5 cm., base menor 1,5 cm. y altura 2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Cálculo del área y del perímetro de un trapecio
(Mueve los vértices del trapecio para variar la medida de los lados)
3. Halla el área y el perímetro de un trapecio rectángulo de base mayor 4,5 cm., base menor 3 cm. y altura 1,2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Cálculo del área y del perímetro de un trapecio rectángulo
4. Halla el área y el perímetro de un trapecio isósceles de base mayor 4 cm., base menor 2,4 cm. y lado L=2 cm.
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Cálculo del área y el perímetro de un trapecio isósceles
(Mueve los vértices del trapecio para variar la medida de los lados) |
|
Actividad: Trapecio
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
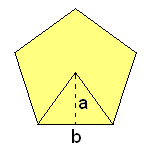
Polígonos regulares
|
|
|
|
Actividad interactiva: Polígono regulares Actividad 1: Deducción del área de un polígono regular. Actividad: Desliza el punto verde y observa
Actividad 2:
Actividad: Contesta en tu cuaderno y comprueba los resultados en la escena siguiente: Calculo del área y del perímetro de un polígono regular.
(Mueve los puntos azules para variar el número de lados y la medida de los mismos)
Pero, para determinar el área, necesitamos conocer, además del lado, la apotema. Si conocemos uno de ellos y el radio, podemos hallar el otro por el Teorema de Pitágoras, como se observa en la siguiente escena: Calculo de la apotema, lado o radio de un polígono regular.
(Mueve los puntos azules para variar el número de lados y la medida de los mismos)
Actividad 3: Cálculo del área y del perímetro de un polígono regular. Actividad: En esta escena puedes comprobar el área, perímetro, apotema y lado de un polígono regular haciendo variar al radio. Desliza el punto verde para modificar el número de lados.
|
|
Actividad: Polígonos regulares
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
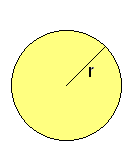
Círculo
|
|
|
|
Actividad interactiva: Círculo Actividad 1: Comprobación de la fórmula de la longitud de la circunferencia. Actividad 2: Aproximación a la fórmula del área del círculo.
Actividad 3: En un círculo de radio 1,71 cm, halla su área y la longitud de su circunferencia.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área y del perímetro de un círculo.
|
|
Actividad: Círculo
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
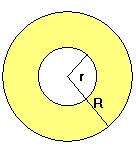
Corona circular
|
|
|
|
Actividad interactiva: Corona circular
1. Halla el área de una corona circular cuyos círculos tienen de radio 2 cm y 1,37 cm, respectivamente.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área de una corona circular
(Mueve el punto azul para modificar el radio pequeño)
|
|
Actividad: Corona circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
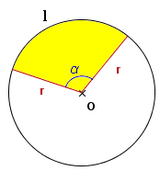
Sector circular
|
|
|
La fórmula del área del sector circular se obtiene a partir de la del área del círculo, aplicando una regla de tres.
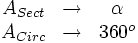
Despejando el área del sector:
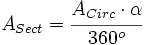
de donde, sustituyendo el área del círculo por su valor, 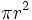 , se obtiene la fórmula.
, se obtiene la fórmula.
Lo mismo ocurre con la de la longitud del arco, que se obtiene a partir de la de la longitud de la circunferencia, también mediante una regla de tres.
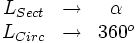
Despejando la longitud del sector:
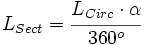
de donde, sustituyendo la longitud de la circunferencia por su valor, 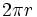 , se obtiene la fórmula.
, se obtiene la fórmula.
|
Actividad interactiva: Sector circular
1. En un círculo de radio 1,80 cm, halla el área de un sector circular de 60º y la longitud de su arco.
Actividad: Haz los cálculos en tu cuaderno y compruébalos en la siguiente escena: Calculo del área de un sector circular
(Mueve el punto B para modificar el ángulo) |
|
Actividad: Sector circular
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
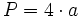
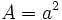
 : lado.
: lado.

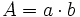
 : base.
: base.
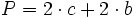
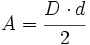

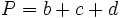
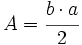
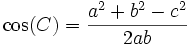
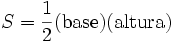
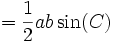
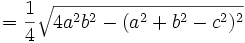
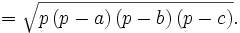
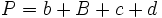
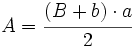
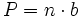
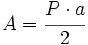
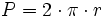
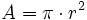
 : número Pi = 3,14159...
: número Pi = 3,14159...
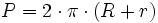
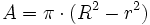
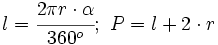
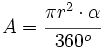
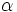 : ángulo (en grados sexagesimales).
: ángulo (en grados sexagesimales).

