Plantilla:Suma de términos de una progresión geométrica

De Wikipedia

(Diferencia entre revisiones)

Saltar a navegación, búsqueda

Revisión de 18:48 25 nov 2016

Suma de términos de una progresión geométrica

La suma de los n primeros términos de una progresión geométrica es:

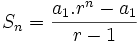
$S_n=\frac{a_1.r^n-a_1}{r-1}$

Demostración:

Efectuamos la siguiente resta:

$r \cdot S_n \qquad ~= \qquad \quad a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n +a_n \cdot r$

$-\;$

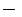
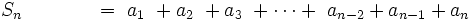
$S_n \ \qquad ~~~~= \ a_1 \ + a_2 \ + a_3 \ + \cdots +\ a_{n-2} + a_{n-1} + a_n$

______________________________________________________________________________

$r \cdot S_n- S_n= -a_1 \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad ~~+a_n \cdot r$

por tanto:

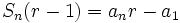
$S_n(r-1)=a_n r-a_1\;$

y despejando

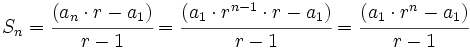
$S_n=\cfrac{(a_n \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^{n-1} \cdot r - a_1)}{r-1}=\cfrac{(a_1 \cdot r^n - a_1)}{r-1}$

Suma de n términos consecutivos de una progresión geométrica (6´48") Sinopsis:

Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica

Autoevaluación: Suma de los términos de una progresión geométrica Descripción:

Suma los n primeros términos de progresión geométrica dada.

Ejercicio resuelto: Suma de términos de una progresión geométrica

Si al comienzo de cada año ingresamos 1000 € en un banco al 4% anual, ¿cuánto dinero tendremos al final del quinto año?

Solución:

Se trata de un problema típico de aritmética comercial de anualidades de capitalización:

Al comenzar el primer año ingreso 1000 €, que se transforman en 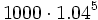$1000 \cdot 1.04^5$ al final del quinto año.

Al comenzar el segundo año ingreso 1000 €, que se transforman en 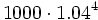$1000 \cdot 1.04^4$ al final del quinto año.

Al comenzar el tercer año ingreso 1000 €, que se transforman en 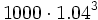$1000 \cdot 1.04^3$ al final del quinto año.

Al comenzar el cuarto año ingreso 1000 €, que se transforman en 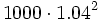$1000 \cdot 1.04^2$ al final del quinto año.

Al comenzar el quinto año ingreso 1000 €, que se transforman en 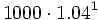$1000 \cdot 1.04^1$ al final del quinto año.

Si sumamos todas esas cantidades:

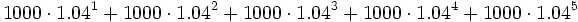
$1000 \cdot 1.04^1 + 1000 \cdot 1.04^2 + 1000 \cdot 1.04^3 + 1000 \cdot 1.04^4 + 1000 \cdot 1.04^5$

estaremos sumando los cinco primeros términos de una progresión geométrica con 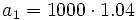$a_1= 1000 \cdot 1.04$ y $r= 1.04\;$

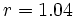
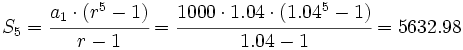$S_5 = \cfrac{a_1 \cdot (r^5 - 1)}{r-1} = \cfrac{1000 \cdot 1.04 \cdot (1.04^5 - 1)}{1.04 -1} = 5632.98$ €

Ejercicios: Anualidades de Capitalización Descripción:

Anualidades de capitalización son cantidades fijas que se entregan al principio de cada año para su colocación a interés compuesto con objeto de llegar a constituir un capital al cabo de un determinado número de años.

Ejercicios: Anualidades de amortización Descripción:

Anualidades de amortización son pagos fijos que se entregan al final de cada año para su colocación a interés compuesto, con objeto de llegar a extinguir o amortizar una deuda juntamente con sus intereses, en un determinado número de años.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Suma_de_t%C3%A9rminos_de_una_progresi%C3%B3n_geom%C3%A9trica"

 |url1=http://matematicasbachiller.com/videos/1-bachillerato/matematicas-de-primero-de-bachillerato/04-sucesiones-aritmeticas-sucesiones-geometricas/07-suma-de-terminos-consecutivos-de-una-sucesion-geometrica#.VCaqh_l_u2E
 |sinopsis=Ejemplos y demostración la fórmula de la suma de n términos consecutivos de una progresión geométrica
+}}
+{{p}}
+{{Geogebra_enlace
+|descripcion=Suma los n primeros términos de progresión geométrica dada.
+|enlace=[https://ggbm.at/k9YG9RFH Autoevaluación: Suma de los términos de una progresión geométrica]
 }}
 {{p}}
 {{p}}
 <center><math>S_5 = \cfrac{a_1 \cdot (r^5 - 1)}{r-1} = \cfrac{1000 \cdot 1.04 \cdot (1.04^5 - 1)}{1.04 -1} = 5632.98</math> €</center>
-}}
-{{p}}
-{{Geogebra_enlace
-|descripcion=Suma los n primeros términos de progresión geométrica dada.
-|enlace=[https://ggbm.at/k9YG9RFH Autoevaluación: Suma de los términos de una progresión geométrica]
 }}
 {{p}}
 |enlace=[https://ggbm.at/ucsDe7EU Ejercicios: Anualidades de Capitalización]
+}}
+{{p}}
+{{Geogebra_enlace
+|descripcion=Anualidades de amortización son pagos fijos que se entregan al final de cada año para su colocación a interés compuesto, con objeto de llegar a extinguir o amortizar una deuda juntamente con sus intereses, en un determinado número de años.
+|enlace=[https://ggbm.at/AC3rw35S Ejercicios: Anualidades de amortización]
 }}

Plantilla:Suma de términos de una progresión geométrica

De Wikipedia

Revisión de 18:48 25 nov 2016

Vistas

Herramientas personales

Menú

Buscar

Herramientas