Plantilla:Tipos de poliedros
De Wikipedia
| Revisión de 09:00 28 nov 2016 Coordinador (Discusión | contribuciones) (→Poliedros convexos y cóncavos) ← Ir a diferencia anterior |
Revisión de 09:02 28 nov 2016 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | |||
| ===Prisma=== | ===Prisma=== | ||
| {{Tabla75|celda1= | {{Tabla75|celda1= | ||
| Línea 91: | Línea 90: | ||
| </table> | </table> | ||
| {{p}} | {{p}} | ||
| - | ===Poliedros duales=== | ||
| - | {{Caja_Amarilla|texto=Dado un poliedro, al unir mediante segmentos los centros de cada dos caras contiguas, se obtiene otro poliedro que se llama el '''poliedro dual''' del dado. | ||
| - | }} | ||
| - | {{p}} | ||
| - | Por ejemplo: | ||
| - | {{p}} | ||
| - | |||
| ===Poliedros regulares=== | ===Poliedros regulares=== | ||
| {{Caja_Amarilla|texto='''Poliedro regular''' es aquel que cumple: | {{Caja_Amarilla|texto='''Poliedro regular''' es aquel que cumple: | ||
| Línea 114: | Línea 106: | ||
| </tr> | </tr> | ||
| </table> | </table> | ||
| + | {{p}} | ||
| + | ===Poliedros duales=== | ||
| + | {{Caja_Amarilla|texto=Dado un poliedro, al unir mediante segmentos los centros de cada dos caras contiguas, se obtiene otro poliedro que se llama el '''poliedro dual''' del dado. | ||
| + | }} | ||
| + | {{p}} | ||
| + | Por ejemplo: | ||
| {{p}} | {{p}} | ||
| ===Poliedros semiregulares=== | ===Poliedros semiregulares=== | ||
Revisión de 09:02 28 nov 2016
Tabla de contenidos |
Prisma
|
Actividades Interactivas: Prismas
1. Tipos de prismas.
Actividad: En esta escena puedes obtener distintos tipos de prismas, variando sus bases, su inclinación y su altura. Experimenta y observa cuantas formas distintas puede adoptar un prisma. No obstante sus bases son siempre paralelas y sus caras laterales paralelogramos.
2. Desarrollo plano de un prisma.
Actividad: En esta escena puedes obtener los desarrollos planos de distintos prismas. Dibújalo en tu cuaderno y contesta:
|
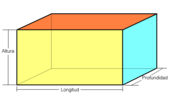
Ortoedro
| Ortoedro
|
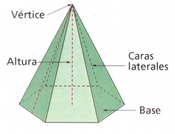
Pirámide
Poliedros simples
Poliedro simple es aquel que no tiene orificios. Un poliedro simple es el que podría hincharse o deformarse (si el material lo permitiera)hasta formar una esfera. En la imagen de la derecha tienes un poliedro que no es simple. Al hincharlo, se transforma en un flotador, en vez de en una esfera. |
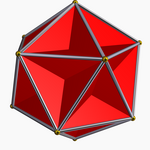
Poliedros convexos y cóncavos
- Un poliedro es convexo si al dados dos puntos cualesquiera del poliedro, el segmento que los une es interior al poliedro. En el caso de que dicho segmento se salga del cuerpo se dice el poliedro es cóncavo.
Son poliedros cóncavos, por ejemplo, los poliedros de Kepler-Poinsot:
Poliedros regulares
Poliedro regular es aquel que cumple:
- Sus caras son polígonos regulares iguales.
- Todos los vértices tienen el mismo orden.
Sólo hay cinco poliedros regulares, los llamados sólidos platónicos:
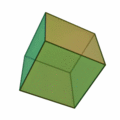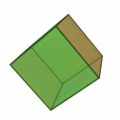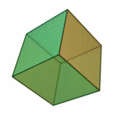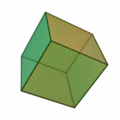
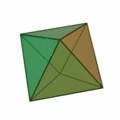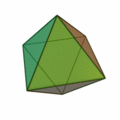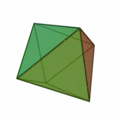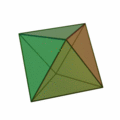
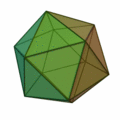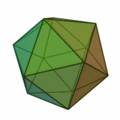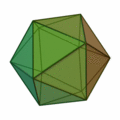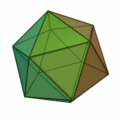
Poliedros duales
Dado un poliedro, al unir mediante segmentos los centros de cada dos caras contiguas, se obtiene otro poliedro que se llama el poliedro dual del dado.
Por ejemplo:
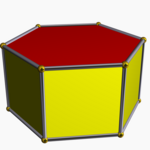
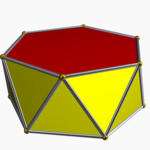
Poliedros semiregulares
Se llama poliedro semiregular a aquel cuyas caras son polígonos regulares de dos o más tipos y tal que en todos los vértices concurren los mismos polígonos.
Son poliedros semiregulares: