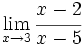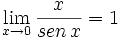Plantilla:Cálculo del límite de una función (1ºBach)
De Wikipedia
| Revisión de 12:19 17 dic 2016 Coordinador (Discusión | contribuciones) (→Límite de una función en un punto en el que se anula el denominador) ← Ir a diferencia anterior |
Revisión de 12:43 17 dic 2016 Coordinador (Discusión | contribuciones) (→Límite en un punto en el que la función es continua) Ir a siguiente diferencia → |
||
| Línea 55: | Línea 55: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| - | {{ejemplo2 | ||
| - | |titulo=Ejemplos: ''Cálculo del límite en un punto en el que la función es continua'' | ||
| - | |enunciado= | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| - | |titulo1=1. Ejemplos | + | |titulo1=Ejemplo de límite inofensivo |
| |duracion=8'03" | |duracion=8'03" | ||
| |sinopsis=:Cálculo de <math>\lim_{x \to 7} \, 4x+2</math> | |sinopsis=:Cálculo de <math>\lim_{x \to 7} \, 4x+2</math> | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0204_01.htm | + | |url1=http://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/02-limites-de-funciones-2/0401-ejemplo-de-limite-inofensivo-4 |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=2. Ejemplos | + | |
| - | |duracion=5'15" | + | |
| - | |sinopsis=:Cálculo de <math>\lim_{x \to 3} \, 6^{\frac{x+2}{x-2}}</math> | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0204_02.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=3. Ejemplos | + | |
| - | |duracion=8'05" | + | |
| - | |sinopsis=:Cálculo de <math>\lim_{x \to 1} \, \sqrt{5-x}</math> | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0204_03.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=4. Ejemplos | + | |
| - | |duracion=3'55" | + | |
| - | |sinopsis=:Cálculo de <math>\lim_{x \to -5} \, ln \, (1-x)</math> | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0204_04.htm | + | |
| - | }} | + | |
| - | {{Video_enlace2 | + | |
| - | |titulo1=5. Ejemplos | + | |
| - | |duracion=11'19" | + | |
| - | |sinopsis={{p}} | + | |
| - | *Cálculo de <math>\lim_{x \to 4} \, sen \, \cfrac{1}{x}</math> | + | |
| - | *Cálculo de <math>\lim_{x \to 0} \, |1-x^2|</math> | + | |
| - | *Cálculo de <math>\lim_{x \to 2} \, \cfrac{x^2 \cdot \sqrt{x-1} \cdot ln \, (1+x^3)}{1+tg^2(x-2)}</math> | + | |
| - | |url1=http://www.matematicasbachiller.com/videos/cdiferencial/df_t_02/vdf0204_05.htm | + | |
| - | }} | + | |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 12:43 17 dic 2016
Tabla de contenidos |
Cálculo del límite de una función en un punto
El cálculo del límite de una función en un punto puede ser muy fácil o muy difícil. Vamos a ver como hay que proceder en cada caso. En los siguientes videos puedes ver algunas nociones previas de interés.
Problema típico: te dan la función "f" y te piden que, si existe, calcules su límite en el punto "c".
- Límites inofensivos: si para calcular f(c) no se viola ninguna Regla Sagrada, la función "f" tiene límite en "c" y coincide con f(c); o sea, existen los dos límites laterales de "f" en "c" y coinciden con f(c).
- Límites peligrosos: si para calcular f(c) se viola ninguna Regla Sagrada, el cálculo del límite de "f" en "c" puede ser muy complicado, y no hay ninguna receta mágica que resuelva el problema en todos los casos.
No debes olvidar que para calcular el límite en un punto nos importa un pito si la función está o no definida en dicho punto, sólo nos interesa que la función está definida en las proximidades del punto.
La operación lógica que llamamos paso al límite (PL) se reduce a conjugar la tercera persona del singular del presente de indicativo del verbo tender.
Recuerda: al escribir x → c (se lee "x" tiende a "c") queremos decir que "x" (o sea, tú) se aproxima a "c" indistintamente por la izquierda o por la derecha.
Este vídeo es muy importante: en él hablamos de operaciones con límites, y las efectuaremos constantemente a partir de ahora.
Límite en un punto en el que la función es continua
El caso más sencillo de cálculo del límite de una función en un punto es aquel en el que la función es continua en dicho punto. En efecto:
Proposición
- Si
 es continua en el punto
es continua en el punto 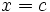 , entonces
, entonces
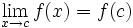
- Es inmediato, por la propia definición de función continua en un punto.
Ejemplo: Cálculo del límite en un punto en el que la función es continua
Calcula:
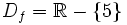 y sabemos que la función es continua en su dominio por ser una función elemental (cociente de funciones polinómicas).
y sabemos que la función es continua en su dominio por ser una función elemental (cociente de funciones polinómicas).
Como 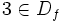 , entonces
, entonces  es continua en 3 y, por tanto:
es continua en 3 y, por tanto:
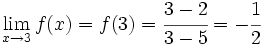
- Cálculo de
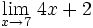
Ejercicios propuestos
|
Ejercicios propuestos: Límite en un punto en el que la función es continua |
Límite de funciones a trozos
Ejemplos: Estudio de la continuidad de una función definida a trozos
2 ejemplos del estudio de la continuidad de una función definida a trozos con parámetros.
Estudio de la continuidad de una función definida a trozos con parámetros.
{{{sol}}}
Límites peligrosos
Vamos a considerar que un límite es "peligroso" o difícil de calcular, si la función en dicho punto no está definida y, por tanto, no podemos aplicar la propiedad de que el valor del límite en un punto en el que la función es continua coincide con el valor de la función en dicho punto.
En este vídeo establecemos el protocolo de actuación cuando al hacer un PL nos encontramos con cualquiera de las siguientes tres situaciones:
- Cociente cuyo denominador tiende a 0, pero no así el númerador.
- Logaritmo de un número que tiende a 0.
- Raíz de índice par de un número que tiende a 0.
Límite de una función en un punto en el que se anula el denominador
Cuando el denominador de la función se anula en el punto en el que queremos calcular el límites se pueden dar dos casos:
Procedimiento
- El numerador no se anula: entonces calcularemos los límites por la derecha y por la izquierda que podrán ser
 ó
ó  . En tal caso el límite podrá no existir (si los límites laterales no coinciden) o podrá der
. En tal caso el límite podrá no existir (si los límites laterales no coinciden) o podrá der  ó
ó  (si los límites laterales coinciden).
(si los límites laterales coinciden).
- El numerador también se anula: entonces tendremos una indeterminación del tipo 0/0. Para resolverla haya que recurrir a técnicas especiales. El caso en el que la función sea racional lo trataremos más adelante.
Ejemplo: Límite de una función en un punto en el que se anula el denominador
Calcula el valor de los siguientes límites:
- a)
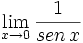 b)
b) 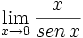
a) No existe el límite porque:
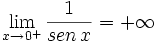 , ya que el denominador tiende a 0 + .
, ya que el denominador tiende a 0 + .
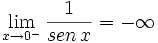 , ya que el denominador tiende a 0 − .
, ya que el denominador tiende a 0 − .
b) El numerador y el denominador tienden a 0 (a esto se le llama una "indeterminación del tipo 0/0"). Usando la calculadora (no tenemos otra herramienta en este curso para este caso), se puede comprobar que:
Puedes hacer uso de la siguiente escena de Geogebra para comprobar la solución:
En esta escena podrás representar funciones definidas en hasta 4 trozos.
Límite de cociente de funciones polinómicas
Siendo la función "f" un cociente de polinomios, en este vídeo vemos dos ejemplos de cálculo del límite de "f" en un punto "c" en que se anula el denominador pero no el numerador.
AVISO: El procedimiento utilizado en este ejercicio excede ligeramente el nivel de 1º de bachillerato.