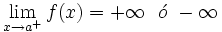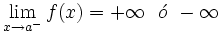Plantilla:Ramas infinitas. Asíntotas (1ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:20 18 dic 2016 Coordinador (Discusión | contribuciones) (→Ramas infinitas) ← Ir a diferencia anterior |
Revisión de 12:34 18 dic 2016 Coordinador (Discusión | contribuciones) (→Ramas infinitas) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| ==Ramas infinitas== | ==Ramas infinitas== | ||
| {{Caja_Amarilla|texto=Decimos que una función <math>f(x)\;</math> presenta una '''rama infinita''' si: | {{Caja_Amarilla|texto=Decimos que una función <math>f(x)\;</math> presenta una '''rama infinita''' si: | ||
| - | #<math>f(x)\,</math> tiende a + infinito o - infinito cuando x tiende a un punto. | + | #<math>f(x)\,</math> tiende a + infinito o - infinito cuando x tiende a un punto por la derecha o por la izquierda. |
| #<math>f(x)\,</math> tiende a + infinito o - infinito cuando x tiende a + infinito o - infinito. | #<math>f(x)\,</math> tiende a + infinito o - infinito cuando x tiende a + infinito o - infinito. | ||
| #<math>f(x)\,</math> tiende a un número real cuando x tiende a + infinito o - infinito. | #<math>f(x)\,</math> tiende a un número real cuando x tiende a + infinito o - infinito. | ||
| Línea 8: | Línea 8: | ||
| {{Caja_Amarilla|texto=Cuando la rama infinita se aproxima a una recta, recibe el nombre de '''asíntota'''.}} | {{Caja_Amarilla|texto=Cuando la rama infinita se aproxima a una recta, recibe el nombre de '''asíntota'''.}} | ||
| {{p}} | {{p}} | ||
| + | {{Tabla3|celda1=[[Imagen:rama1.png|center|250px]]{{p}}<center><math>\lim_{x \to 1^+} \cfrac{1}{x-1}=+\infty</math></center> | ||
| + | |celda2=[[Imagen:rama2.gif|center|250px]]{{p}}<center><math>\lim_{x \to +\infty} x^3=+\infty</math></center> | ||
| + | |celda2=[[Imagen:rama3.png|center|250px]]{{p}}<center><math>\lim_{x \to +\infty} x^3=+\infty</math></center> | ||
| + | }} | ||
| ===Ramas infinitas cuando x tiene a un punto: Asíntotas verticales=== | ===Ramas infinitas cuando x tiene a un punto: Asíntotas verticales=== | ||
| {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> presenta en <math>x=a\;</math> una '''asíntota vertical''' (A.V.) si ocurre alguna de estas dos cosas: | {{Caja_Amarilla|texto=Una función <math>f(x)\;</math> presenta en <math>x=a\;</math> una '''asíntota vertical''' (A.V.) si ocurre alguna de estas dos cosas: | ||
Revisión de 12:34 18 dic 2016
Tabla de contenidos |
Ramas infinitas
Decimos que una función  presenta una rama infinita si:
presenta una rama infinita si:
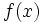 tiende a + infinito o - infinito cuando x tiende a un punto por la derecha o por la izquierda.
tiende a + infinito o - infinito cuando x tiende a un punto por la derecha o por la izquierda.
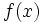 tiende a + infinito o - infinito cuando x tiende a + infinito o - infinito.
tiende a + infinito o - infinito cuando x tiende a + infinito o - infinito.
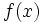 tiende a un número real cuando x tiende a + infinito o - infinito.
tiende a un número real cuando x tiende a + infinito o - infinito.
Cuando la rama infinita se aproxima a una recta, recibe el nombre de asíntota.
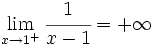 | 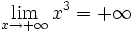 | {{{celda3}}} |
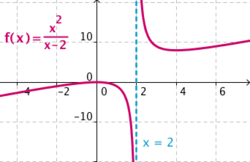
Ramas infinitas cuando x tiene a un punto: Asíntotas verticales
Una función  presenta en
presenta en  una asíntota vertical (A.V.) si ocurre alguna de estas dos cosas:
una asíntota vertical (A.V.) si ocurre alguna de estas dos cosas:
La gráfica de la función se acerca a la recta  (asíntota vertical), al aproximarse la variable
(asíntota vertical), al aproximarse la variable  al punto
al punto  .
.
Ramas infinitas cuando x tiene a infinito
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas |
Ramas infinitas de las funciones racionales
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas de las funciones racionales |
Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas
Ejercicios propuestos
|
Ejercicios propuestos: Ramas infinitas de las funciones trigonométricas, exponenciales y logarítmicas |