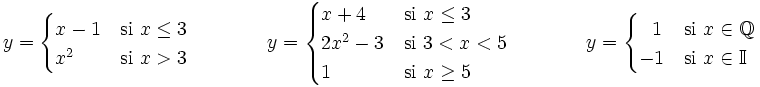Plantilla:Funciones definidas a trozos
De Wikipedia
| Revisión de 06:47 29 mar 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:59 27 abr 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 27: | Línea 27: | ||
| <center><math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math></center> | <center><math>y = \begin{cases} x-3 & \mbox{si }x \le 0 \\ ~~2 & \mbox{si }0<x<3 \\ -x & \mbox{si }x \ge 3 \end{cases}</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_unicoos | ||
| + | |titulo1=La función signo | ||
| + | |duracion=4'51" | ||
| + | |sinopsis=Un ejemplo de función a trozos. | ||
| + | |url1=http://www.unicoos.com/video/matematicas/4-eso/funciones-elementales/funcion-signo/funcion-signo-01 | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 09:59 27 abr 2017
Una función definida a trozos es aquella que utiliza varias funciones para su definición, cada una de ellas definida en un determinado subconjunto del dominio de definición de la función principal.
Son funciones definidas a trozos:
Ejemplos: Función definida a trozos
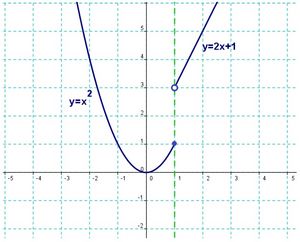
Representa la siguiente función:
Para su representación, tenemos que dibujar cada una de las funciones en sus respectivos tramos, prestando especial atención a los puntos de "empalme" (extremos de los intervalos de definición).
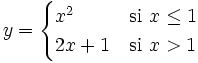
Ejemplos: Función definida a trozos
Encuentra la expresión analítica de la función cuya gráfica es la siguiente:
Tendremos que hallar las ecuaciones de tres rectas. Para ello localizaremos dos puntos por los que pase cada recta y a partir de ellos obtendremos su pendiente y luego su ecuación por medio de la ecuación punto-pendiente.
La función signo (4'51") Sinopsis: Un ejemplo de función a trozos.
Función definida a trozos Descripción: En esta escena podrás representar funciones definidas en hasta 4 trozos.
