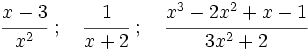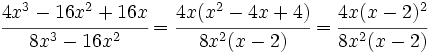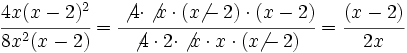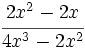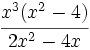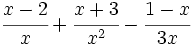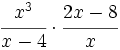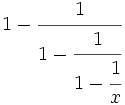Plantilla:Fracciones algebraicas

De Wikipedia

(Diferencia entre revisiones)

Revisión de 09:48 6 may 2017

Tabla de contenidos

1 Fracción algebraica
- 1.1 Fracciones algebraicas equivalentes
2 Simplificación de fracciones algebraicas
3 Suma y resta de fracciones algebraicas
4 Producto de fracciones algebraicas
5 Cociente de fracciones algebraicas
6 Actividades

Fracción algebraica

Una fracción algebraica es una expresión fraccionaria en la que numerador y denominador son polinomios, siendo el denominador no nulo.

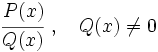
$\cfrac{P(x)}{Q(x)} ~, \quad Q(x) \ne 0$

Ejemplos

Son fracciones algebraicas:

$\cfrac{x-3}{x^2}\ ;\quad \cfrac{1}{x+2}\ ; \quad \cfrac{x^3-2x^2+x-1}{3x^2+2}$

Las fracciones algebraicas tienen un comportamiento similar a las fracciones niuméricas a la hora de trabajar con ellas.

Fracciones algebraicas equivalentes

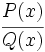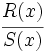Dos fracciones algebraicas $\cfrac{P(x)}{Q(x)}$ y $\cfrac{R(x)}{S(x)}$ son equivalentes si

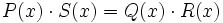
$P(x) \cdot S(x)= Q(x) \cdot R(x)$

Ejemplo

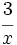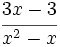Las fracciones algebraicas $\cfrac{3}{x}$ y $\cfrac{3x-3}{x^2-x}$ , son equivalentes:

En efecto, si hacemos los productos cruzados:

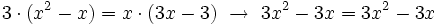
$3 \cdot (x^2-x) = x \cdot (3x-3) \ \rightarrow \ 3x^2-3x = 3x^2-3x$

estos coinciden.

Simplificación de fracciones algebraicas

Procedimiento

Para simplificar fracciones algebraicas, se factorizan numerador y denominador y se simplifican los factores comunes. La fracción algebraica así obtenida es equivalente a la de partida.

Ejemplos: Simplificar fracciones algebraicas

Simplifica: 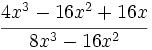$\cfrac {4x^3-16x^2+16x}{8x^3-16x^2}$

Solución:

Primero factorizamos numerador y denominador:

$\cfrac {4x^3-16x^2+16x}{8x^3-16x^2} = \cfrac {4x(x^2-4x+4)}{8x^2(x-2)} = \cfrac {4x(x-2)^2}{8x^2(x-2)}$

A continuación simplificamos los factores comunes al numerador y denominador:

$\cfrac {4x(x-2)^2}{8x^2(x-2)}=\cfrac {\not{4} \cdot \not{x} \cdot (x \!\! \not{-} \, 2) \cdot (x-2)}{\not{4} \cdot 2 \cdot \not{x} \cdot x \cdot (x \!\! \not{-} \, 2)}= \cfrac {(x-2)}{2x}$

Ejemplo 1 (2´35") Sinopsis:

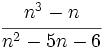
Simplifica: $\cfrac{n^3-n}{n^2-5n-6}$

Ejemplo 2 (3´12") Sinopsis:

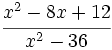
Simplifica: $\cfrac{x^2-8x+12}{x^2-36}$

Problema 1 (4´57") Sinopsis:

Problema que requiere simplificar fracciones algebraicas

Simplificación de fracciones algebraicas

Actividad: Simplificación de fracciones algebraicas

Simplifica:

a) $\cfrac{2x^2-2x}{4x^3-2x^2}$

b) $\cfrac{x^3(x^2-4)}{2x^2-4x}$

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) simplify (2x^2-2x)/(4x^3-2x^2)

b) simplify (x^3*(x^2-4))/(2x^2-4x)

Fracciones algebraicas. Equivalencia y simplificación. (4´47") Sinopsis:

Si P(x) y Q(x) son polinomios y Q(x) no es el polinomio nulo, llamamos fracción algebraica a toda expresión de la forma P(x)/Q(x).
Las fracciones algebraicas A(x)/B(x) y C(x)/D(x) se dicen equivalentes si A(x).D(x) = C(x).D(x), y se escribe A(x)/B(x) = C(x)/D(x).
Si el numerador y el denominador de una fracción algebraica se multiplican por un polinomio no nulo, resulta una fracción algebraica equivalente.
Si el numerador y el denominador de una fracción algebraica son divisibles por un mismo polinomio, y se dividen, resulta una fracción algebraica equivalente, diciéndose que la primera fracción algebraica se ha "simplificado".

3 ejercicios sobre equivalencia de fracciones algebraicas (5´46") Sinopsis:

Videotutorial.

4 ejercicios sobre simplificación de fracciones algebraicas (6´14") Sinopsis:

Videotutorial.

Suma y resta de fracciones algebraicas

Para sumar y restar procederemos de forma similar que con fracciones de números enteros, reduciendo primero a común denominador.

Ejemplos: Suma y resta de fracciones algebraicas

Opera: 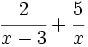$\cfrac {2}{x-3} + \cfrac {5}{x}$

Solución:

Reducimos a común denominador ambas fracciones, usando el m.c.m. de los denominadores que es 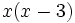$x(x-3) \;\!$

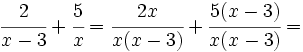
$\cfrac {2}{x-3} + \cfrac {5}{x} = \cfrac {2x}{x(x-3)} + \cfrac {5(x-3)}{x(x-3)}=$

Sumamos los numeradores dejando el mismo denominador y simplificamos el numerador:

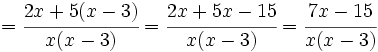
$=\cfrac {2x+5(x-3)}{x(x-3)}=\cfrac {2x+5x-15}{x(x-3)}=\cfrac {7x-15}{x(x-3)}$

Suma y resta de fracciones algebraicas (6´39") Sinopsis:

Suma y resta de fracciones algebraicas. Ejemplos

Ejemplo de suma y resta de fracciones algebraicas (6´48") Sinopsis:

Opera y simplifica: 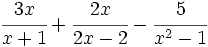$\cfrac{3x}{x+1}+\cfrac{2x}{2x-2}-\cfrac{5}{x^2-1}$

En este ejemplo se verá la utilidad de usar el m.c.m. frente a no usarlo.

Ejercicio 1: Suma de fracciones algebraicas (3´50") Sinopsis:

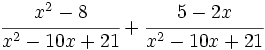
Opera y simplifica: $\cfrac{x^2-8}{x^2-10x+21}+\cfrac{5-2x}{x^2-10x+21}$

Ejercicio 2: Suma de fracciones algebraicas (8´05") Sinopsis:

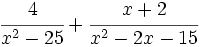
Opera y simplifica: $\cfrac{4}{x^2-25}+\cfrac{x+2}{x^2-2x-15}$

Ejercicio 3: Suma de fracciones algebraicas (9´46") Sinopsis:

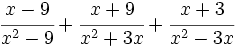
Opera y simplifica: $\cfrac{x-9}{x^2-9}+\cfrac{x+9}{x^2+3x}+\cfrac{x+3}{x^2-3x}$

Ejercicio 4: Resta de fracciones algebraicas (6´56") Sinopsis:

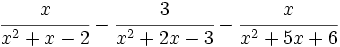
Opera y simplifica: $\cfrac{x}{x^2+x-2}-\cfrac{3}{x^2+2x-3}-\cfrac{x}{x^2+5x+6}$

Producto de fracciones algebraicas

Para multiplicar fracciones algebraicas procederemos igual que con fracciones, multiplicando los numeradores y los denominadores, aunque antes de multiplicar debemos simplificar, si se puede.

Ejemplos: Producto de fracciones algebraicas

Opera: 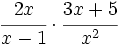$\cfrac {2x}{x-1} \cdot \cfrac {3x+5}{x^2}$

Solución:

Multiplicamos numeradores y denominadores, pero lo dejamos indicado:

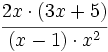
$\cfrac {2x \cdot (3x+5)}{(x-1) \cdot x^2 }$

Simplificamos antes de efectuar el producto:

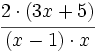
$\cfrac {2 \cdot (3x+5)}{(x-1) \cdot x }$

Finalmente, podemos multiplicar, si es preciso:

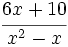
$\cfrac {6x+10}{x^2-x}$

Ejercicio 1: Producto de fracciones algebraicas (9´44") Sinopsis:

Opera y simplifica: 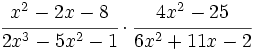$\cfrac {x^2-2x-8}{2x^3-5x^2-1} \cdot \cfrac {4x^2-25}{6x^2+11x-2}$

Cociente de fracciones algebraicas

Para dividir fracciones algebraicas procederemos igual que con fracciones, haciendo el producto cruzado de numeradores y denominadores, aunque antes de multiplicar debemos simplificar, si se puede.

Ejemplos: Cociente de fracciones algebraicas

Opera: 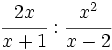$\cfrac{2x}{x+1}:\cfrac{x^2}{x-2}$

Solución:

Hacemos el producto cruzado, dejándolo indicado:

$\cfrac {2x \cdot (x-2)}{(x+1) \cdot x^2}$

Simplificamos:

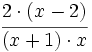
$\cfrac {2 \cdot (x-2)}{(x+1) \cdot x}$

Finalmente, podemos multiplicar, si es preciso:

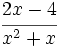
$\cfrac {2x-4}{x^2+x}$

Producto y cociente de fracciones algebraicas (3´21") Sinopsis:

Producto y cociente de fracciones algebraicas. Ejemplos

Ejercicio 1: Cociente de fracciones algebraicas (4´03") Sinopsis:

Opera y simplifica: 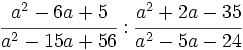$\cfrac {a^2-6a+5}{a^2-15a+56}:\cfrac {a^2+2a-35}{a^2-5a-24}$

Actividades

Ejercicios resueltos: Operaciones con fracciones algebraicas

Opera:

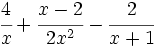
1. $\cfrac {4}{x}+\cfrac {x-2}{2x^2}-\cfrac {2}{x+1}$

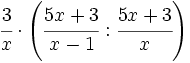
2. $\cfrac {3}{x} \cdot \left ( \cfrac {5x+3}{x-1}:\cfrac {5x+3}{x} \right )$

Solución:

Soluciones:

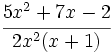
1. $\cfrac {5x^2+7x-2}{2x^2(x+1)}$

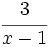
2. $\cfrac {3}{x-1}$

Operaciones con fracciones algebraicas

Actividad: Operaciones con fracciones algebraicas

Opera:

a) $\cfrac{x-2}{x}+\cfrac{x+3}{x^2}-\cfrac{1-x}{3x}$

b) $\cfrac{x^3}{x-4} \cdot \cfrac{2x-8}{x}$

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) simplify (x-2)/x+(x+3)/x^2-(1-x)/(3x)

b) simplify ((x^3)/(x-4))*((2x-8)/x)

Ejercicio 1: Operaciones con fracciones algebraicas (3´41") Sinopsis:

Simplifica: $\cfrac {1+\cfrac{1}{c-1}}{1-\cfrac{1}{c-1}}$

Ejercicio 2: Operaciones con fracciones algebraicas (3´07") Sinopsis:

Simplifica: $\cfrac {x^{-1}+y^{-1}}{(x+y)^{-1}}$

Ejercicio 3: Operaciones con fracciones algebraicas (6´54") Sinopsis:

Simplifica: $\cfrac {2x^{-1}y+2xy^{-1}}{2(x^{-2}+y^{-2})}$

Ejercicio 4: Operaciones con fracciones algebraicas (4´48") Sinopsis:

Simplifica:

$1-\cfrac {1}{1-\cfrac{1}{1-\cfrac{1}{x}}}$

Ejercicio 5: Simplificación de potencias con fracciones algebraicas (7´28") Sinopsis:

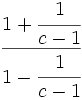
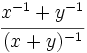
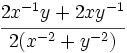
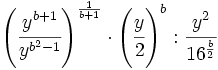
Simplifica: $\left(\cfrac {y^{b+1}}{y^{b^2-1}} \right)^{\frac{1}{b+1}} \cdot \left(\cfrac {y}{2} \right)^b : \cfrac {y^2}{16^{\frac{b}{2}}}$

Ejercicio 6: Simplificación de potencias con fracciones algebraicas (6´50") Sinopsis:

Simplifica: $\left[ \left(\cfrac {x}{x^a} \right)^a \cdot \left(\cfrac {x^{2a}}{x^{a+1}} \right) \cdot \left(\cfrac {xâ}{x^{-1}} \right)^{a+1} \right]^{\frac{1}{a}}$

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Fracciones_algebraicas"

 |duracion=4´48"
 |url1=https://www.youtube.com/watch?v=8ksc9IMxCSc&index=73&list=PL9B9AC3136D2D4C45
-|sinopsis=Videotutorial.
+|sinopsis=Simplifica:
+:<math>1-\cfrac {1}{1-\cfrac{1}{1-\cfrac{1}{x}}}</math>
 }}
-{{p}}
 {{p}}
 {{Video_enlace_julioprofe
 |duracion=7´28"
 |url1=https://www.youtube.com/watch?v=4DdNIvYHMoY&index=74&list=PL9B9AC3136D2D4C45
-|sinopsis=Videotutorial.
+|sinopsis=Simplifica: <math>\left(\cfrac {y^{b+1}}{y^{b^2-1}} \right)^{\frac{1}{b+1}} \cdot \left(\cfrac {y}{2} \right)^b : \cfrac {y^2}{16^{\frac{b}{2}}} </math>
 }}
 {{p}}
 |duracion=6´50"
 |url1=https://www.youtube.com/watch?v=-FoAgr01OnA&index=75&list=PL9B9AC3136D2D4C45
-|sinopsis=Videotutorial.
+|sinopsis=Simplifica: <math>\left[ \left(\cfrac {x}{x^a} \right)^a \cdot \left(\cfrac {x^{2a}}{x^{a+1}} \right) \cdot \left(\cfrac {xâ}{x^{-1}} \right)^{a+1} \right]^{\frac{1}{a}} </math>
 }}
 {{p}}

Plantilla:Fracciones algebraicas

De Wikipedia

Revisión de 09:48 6 may 2017

Tabla de contenidos

Fracción algebraica

Fracciones algebraicas equivalentes

Simplificación de fracciones algebraicas

Suma y resta de fracciones algebraicas

Producto de fracciones algebraicas

Cociente de fracciones algebraicas

Actividades

Vistas

Herramientas personales

Menú

Buscar

Herramientas