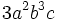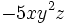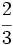Plantilla:Monomios
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:51 11 may 2017 Coordinador (Discusión | contribuciones) (→Monomios semejantes) ← Ir a diferencia anterior |
Revisión de 06:57 12 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 19: | Línea 19: | ||
| <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Polinomios/monomios_2.html '''Click''' aquí si no se ve bien la escena]</center> | <center>[http://maralboran.org/web_ma/descartes/Bach_CNST_1/Polinomios/monomios_2.html '''Click''' aquí si no se ve bien la escena]</center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Video_enlace_paps | ||
| + | |titulo1=Grado de un monomio | ||
| + | |duracion=3'48" | ||
| + | |sinopsis=Aprende a calcular el grado de un monomio | ||
| + | |url1=https://www.youtube.com/watch?v=ziPklrOtsNk | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 06:57 12 may 2017
- Monomio es una expresión algebraica en la que aparece el producto de un número por una o varias letras elevadas a potencias de exponente natural.
- Se llama coeficiente de un monomio al número que aparece multiplicando a las letras. Normalmente se coloca al principio. Si el coeficiente es un 1 no suele escribirse. Si el coeficiente es 0, el monomio resultante es el número 0.
- Se denomina grado de un monomio a la suma de los exponentes de las letras. Si no hay letras el grado es cero.
- a)
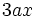es un monomio de grado 2 y coeficiente 3.
- b)
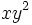es un monomio de grado 3 y coeficiente 1.
- c)
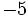es un monomio de grado 0 y coeficiente -5.
- d) En la siguiente escena se puede observar el coeficiente y el grado de un monomio. En la parte superior se pueden cambiar los exponentes de las letras a, b, y x. Para cambiar el coeficiente del monomio modifica la casilla de abajo.
Grado de un monomio (3'48") Sinopsis: Aprende a calcular el grado de un monomio
Monomios semejantes
Son monomios semejantes aquellos en los que aparecen las mismas letras con los mismos exponentes.
Son monomios semejantes: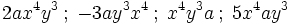 
Las letras pueden aparecer en distinto orden ya que por la propiedad conmutativa las podemos reordenar.
Términos semejantes (4'45") Sinopsis: Aprende a distiguir cuando dos monomios son o no semejantes.
Términos semejantes (5'11") Sinopsis: Aprende a distiguir cuando dos monomios son o no semejantes.
Actividad: Grado de un monomio Indica el grado y el coeficiente de los siguientes monomios:
Solución: Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:
|
