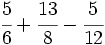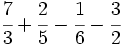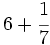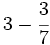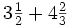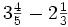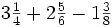Plantilla:Ejemplo suma fracciones
De Wikipedia
| Revisión de 16:26 18 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:27 18 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 46: | Línea 46: | ||
| |titulo1=Ejemplos 2 | |titulo1=Ejemplos 2 | ||
| |duracion=7'26" | |duracion=7'26" | ||
| - | |sinopsis=Suma y resta de fracciones con distinto denominador. | + | |sinopsis=Suma y resta de fracciones con distinto denominador(método del m.c.m.). |
| a) <math>\cfrac{1}{3}+ \cfrac{1}{6}</math>{{b4}}{{b4}}b) <math>\cfrac{3}{4}- \cfrac{3}{5}</math> | a) <math>\cfrac{1}{3}+ \cfrac{1}{6}</math>{{b4}}{{b4}}b) <math>\cfrac{3}{4}- \cfrac{3}{5}</math> | ||
Revisión de 16:27 18 may 2017
Ejemplo: Suma y resta de fracciones
Calcula: 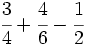
Solución:
Calculamos el m.c.m. de los denominadores:
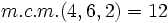
y reducimos las fracciones a común denominador:
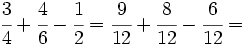
Una vez que tenemos las fracciones homogéneas, sumamos o restamos los númeradores, dejando el mismo denominador:
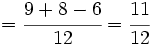
Suma de fracciones con el mismo denominador. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Otro método para sumar o restar fracciones, fácil de recordar, que no requiere del m.c.m, pero que a veces precisa simplificar más al final. Lo que en este video se explica es válido para la resta sin más que cambiar suma por resta.
Suma y resta de fracciones con el mismo denominador:
a) 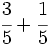 b)
b) 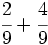 c)
c) 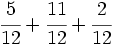 d)
d) 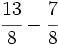 e)
e) 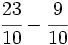
Suma y resta de fracciones con distinto denominador(método del m.c.m.).
a) 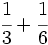 b)
b) 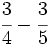
Suma de fracciones con distinto denominador.
a) 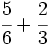 b)
b) 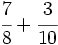 c)
c) 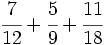
Suma y resta de fracciones con distinto denominador.
Suma y resta de cuatro fracciones con distinto denominador usando el método del m.c.m.:
Suma de un entero y una fracción:
Resta de un entero y una fracción.
Suma de números mixtos.
Resta de números mixtos.
Suma y resta de números mixtos.