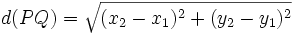Plantilla:Cálculo de la distancia entre dos puntos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:57 19 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:07 19 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 3: | Línea 3: | ||
| {{Caja|contenido=<math>d(PQ)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}</math>}} | {{Caja|contenido=<math>d(PQ)=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}</math>}} | ||
| - | |demo=Ver la siguiente escena de Geogebra. | + | |demo=Ver el siguiente videotutorial: |
| - | }} | + | |
| - | {{p}} | + | |
| - | {{Geogebra: distancia entre dos puntos}} | + | |
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| |titulo1=Distancia entre dos puntos | |titulo1=Distancia entre dos puntos | ||
| Línea 13: | Línea 10: | ||
| |url1=https://www.youtube.com/watch?v=mC7-joiQsK4 | |url1=https://www.youtube.com/watch?v=mC7-joiQsK4 | ||
| }} | }} | ||
| + | }} | ||
| + | {{p}} | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Distancia entre dos puntos | + | |titulo1=Ejemplo |
| |duracion=6'12" | |duracion=6'12" | ||
| - | |sinopsis=Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos. | + | |sinopsis=Ejemplo que ilustra la posterior demostración de la fórmula de la distancia entre dos puntos del plano. |
| |url1=https://www.youtube.com/watch?v=ZPR5WeYv3B4&list=PLHwz3md30-3kyfZgB4y53rPmPydQwj6uj&index=3 | |url1=https://www.youtube.com/watch?v=ZPR5WeYv3B4&list=PLHwz3md30-3kyfZgB4y53rPmPydQwj6uj&index=3 | ||
| }} | }} | ||
| + | {{Geogebra: distancia entre dos puntos}} | ||
| {{p}} | {{p}} | ||
Revisión de 11:07 19 may 2017
Conocidas las coordenadas de dos puntos del plano, el teorema de Pitágoras nos permite calcular la distancia entre ambos:
Proposición
La distancia entre dos puntos 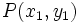 y
y 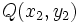 es igual a:
es igual a:
|
|
Demostración:
Ver el siguiente videotutorial:
Demostración de la fórmula de la distancia entre dos puntos del plano. Ejemplos.
Ejemplo que ilustra la posterior demostración de la fórmula de la distancia entre dos puntos del plano.
En esta escena podrás ver como se calcula la distancia entre dos puntos del plano.