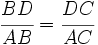Plantilla:Aplicaciones de los criterios de semejanza
De Wikipedia
| Revisión de 16:01 24 may 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:02 24 may 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 37: | Línea 37: | ||
| - | '''Solución:''' Este problema requiere la aplicación del teorema de la mediana relativa a la hipotenusa de un triángulo rectángulo. Véase el video para ver la solución. | + | '''Solución:''' Véase el video para ver la solución. |
| }} | }} | ||
| ---- | ---- | ||
| {{Tabla75|celda2=[[Imagen:medianahipotenusa.png|300px]]|celda1= | {{Tabla75|celda2=[[Imagen:medianahipotenusa.png|300px]]|celda1= | ||
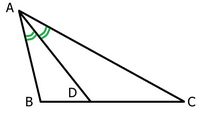
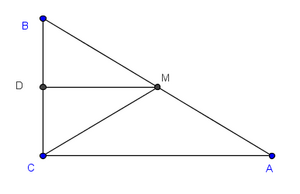
| + | El problema anterior requiere la aplicación del teorema de la mediana relativa a la hipotenusa de un triángulo rectángulo: | ||
| + | |||
| '''Teorema de la mediana relativa a la hipotenusa:''' | '''Teorema de la mediana relativa a la hipotenusa:''' | ||
Revisión de 16:02 24 may 2017
Los criterios de semejanza que hemos visto tienen numerosas aplicaciones. Veamos algunas de ellas.
Medición de alturas con espejos Descripción: En esta escena podrás hallar la altura de una casa utilizando un espejo y una cinta métrica.
Medición de alturas con sombras Descripción: Cuenta la historia que un sacerdote egipcio le preguntó a Tales de Mileto (s. IV a. C) acerca de la altura de la Pirámide de Keops, cuando ya las pirámides rondaban los 2.000 años de edad, y éste respondió con un método de lo más ingenioso para medir dicha altura..
Teorema de la bisectriz (8´43") Sinopsis: El teorema de la bisectriz dice:
"La bisectriz de un ángulo de un triángulo divide al lado opuesto en dos segmentos que son proporcionales a los otros dos lados del triángulo"
 | 
|
Problema (aplicación del teorema de la bisectriz) (5´46") Sinopsis: Aplicación del teorema de la bisectriz.
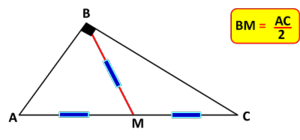
Teorema de la mediana relativa a la hipotenusa (8´00") Sinopsis:| Problema:
Halla el valor de "x" en la figura:
Solución: Véase el video para ver la solución. |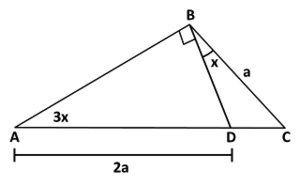 
|
| El problema anterior requiere la aplicación del teorema de la mediana relativa a la hipotenusa de un triángulo rectángulo:
Teorema de la mediana relativa a la hipotenusa: "La longitud de la mediana relativa a la hipotenusa de un triángulo rectángulo, es igual a la mitad de la longitud de la hipotenusa." | 
|
| Demostración:
Por M tracemos una paralela a CA, y sea D su punto de intersección con el cateto BC. Puesto que DM es paralela a CA y CA es perpendicular a BC, entonces DM es también perpendicular a BC. Los triángulos BDM y BCA semejantes por estar en la posición de Thales, de manera que se tiene que D es punto medio de BC (ya que M lo es de AB). Pero entonces DM es mediatriz de BCM. De aquí que BM=CM (pues la mediatriz de un segmento es el lugar geométrico de los puntos que equidistan de los extremos). | 
|
