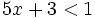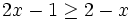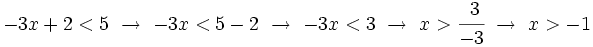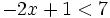Plantilla:Inecuaciones lineales con una incógnita
De Wikipedia
| Revisión de 09:41 28 may 2017 Coordinador (Discusión | contribuciones) (→Método algebraico de resolución) ← Ir a diferencia anterior |
Revisión de 09:49 28 may 2017 Coordinador (Discusión | contribuciones) (→Método algebraico de resolución) Ir a siguiente diferencia → |
||
| Línea 150: | Línea 150: | ||
| |url1=https://www.youtube.com/watch?v=KdasymEoL6A&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=17 | |url1=https://www.youtube.com/watch?v=KdasymEoL6A&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo&index=17 | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 16 | ||
| + | |duracion=4'30" | ||
| + | |sinopsis=Resuelve: <math>(2x-3)(5+x) \le (1+x)(2x+3)\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=rZOjDFdrKgM&index=28&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | ||
| + | }} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Ejercicio 17 | ||
| + | |duracion=5'16" | ||
| + | |sinopsis=Resuelve: <math>(x+2)^2 > (x+3)(x+2)\;</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=qF267wzM97E&index=29&list=PL9SnRnlzoyX3WSvCry-ctW4l_yMH1Z9Xo | ||
| }} | }} | ||
| }} | }} | ||
Revisión de 09:49 28 may 2017
Una inecuación lineal con una incógnita es una inecuación, en la que las expresiones matemáticas que intervienen en la desigualdad, son polinomios de primer grado en una sola variable. En consecuencia, puede ponerse, mediante transformaciones, de alguna de estas formas:
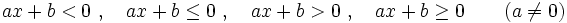
donde 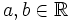 son los coeficientes y
son los coeficientes y  es la variable.
es la variable.
Resolución de una inecuación lineal con una incógnita
Método algebraico de resolución
El método algebraico aplica las anteriores transformaciones para conseguir dejar despejada la incógnita.
Ejemplo: Inecuaciones lineales con una incógnita (método algebraico)
Resuelve la siguiente inecuación:
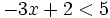
- Solución:
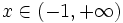
Resuelve:
- a)
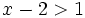
- b)
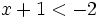
- c)
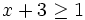
Resuelve:
- a)
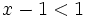
- b)
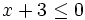
- c)
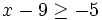
Resuelve:
- a)
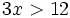
- b)
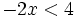
- c)
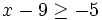
Resuelve:
- a)
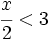
- b)
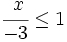
- c)
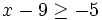
Resuelve: 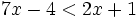
Resuelve: 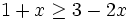
Resuelve: 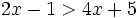
Resuelve: 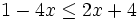
Resuelve: 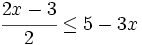
Resuelve: 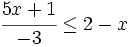
Resuelve: 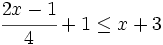
Resuelve: 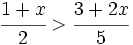
Resuelve: 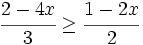
Resuelve: 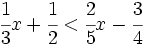
Resuelve: 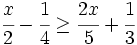
Resuelve: 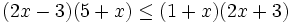
Resuelve: 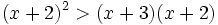
Autoevaluación sobre inecuaciones lineales.
Autoevaluación sobre inecuaciones lineales.
Método gráfico de resolución
Inecuaciones lineales con una incógnita (método gráfico)
Las soluciones de una inecuación lineal con una incógnita son los puntos de la semirrecta que se encuentra a uno de los dos lados del punto de corte de la recta 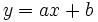 con el eje de abscisas, es decir del punto
con el eje de abscisas, es decir del punto 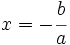 .
.
En una de las semirrectas con origen ese punto se cumple la condición 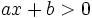 y en la otra, la condición
y en la otra, la condición 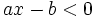 .
.
Así, para determinar la semirrecta solución, basta con fijarse en los valores de la variable x para los que la recta 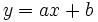 está por encima o por debajo del eje de abscisas.
está por encima o por debajo del eje de abscisas.
Si la inecuación no es estricta, el punto del extremo de la semirrecta, 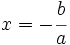 , es también solución, ya que para él se verifica la igualdad.
, es también solución, ya que para él se verifica la igualdad.
En la escena resolveremos la siguiente inecuación por el método gráfico:
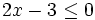
Para ello representamos la recta 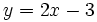 y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.
y nos fijamos para que valores de x, la gráfica está por debajo del eje X (es negativa) o vale cero.