Plantilla:Radicales (nivel básico)
De Wikipedia
| Revisión de 09:11 29 may 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las operaciones con radicales) ← Ir a diferencia anterior |
Revisión de 09:35 29 may 2017 Coordinador (Discusión | contribuciones) (→Suma y resta de radicales semejantes) Ir a siguiente diferencia → |
||
| Línea 168: | Línea 168: | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| + | {{Video_enlace_matefacil | ||
| + | |titulo1=Suma y resta de radicales semejantes | ||
| + | |duracion=4'58" | ||
| + | |sinopsis=Suma y resta de radicales semejantes. Ejemplos. | ||
| + | |url1=https://www.youtube.com/watch?v=zlR_Pq5BWME&index=11&list=PL9SnRnlzoyX3PUSesWagsxJdOfANgK_LO | ||
| + | }} | ||
Revisión de 09:35 29 may 2017
Tabla de contenidos |
Radical
- Un radical es cualquier expresión del tipo:
![k \cdot \sqrt[n]{a}~,~k \in \mathbb{R}](/wikipedia/images/math/c/2/6/c26445b313b501056047ed7787606a37.png)
- Si dos radicales tienen el mismo índice diremos que son homogéneos.
- Si dos radicales tienen el mismo índice y el mismo radicando diremos que son semejantes.
Radicales: homogéneos y semejantes. Ejemplos.
Operaciones con radicales
Propiedades de las operaciones con radicales
Propiedades de las operaciones con radicales
1. ![\sqrt[np]{a^p}=\sqrt[n]{a}](/wikipedia/images/math/1/9/0/19055926ec943d41884a4e4efb9e3958.png)
2. ![\left ( \sqrt[n]{a}\right )^p=\sqrt[n]{a^p}](/wikipedia/images/math/0/8/f/08f48fff6b28e5860652ad48624e9b54.png)
3. ![\sqrt[m]{\sqrt[n]{a}}=\sqrt[mn]{a}](/wikipedia/images/math/8/8/2/882098878748f7e317a403bacf091e37.png)
4. ![\sqrt[n]{a} \cdot \sqrt[n]{b}=\sqrt[n]{a \cdot b}](/wikipedia/images/math/7/3/d/73d577cd0a118df1dda404e72e4a922d.png)
5. ![\cfrac{\sqrt[n]{a}}{\sqrt[n]{b}}=\sqrt[n]{\cfrac{a}{b}}](/wikipedia/images/math/4/8/d/48d4191b86a6079638a33f860884bd8e.png)
Para demostrar estas propiedades basta con expresar el radical como potencia de exponente fraccionario y aplicar sus propiedades.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Pulsa el botón "Ejemplo" para ver los ejemplos. Anota algunos en tu cuaderno.
Ejercicios resueltos: Radicales. Propiedades
Simplificar: a) ![\sqrt[12]{x^9}](/wikipedia/images/math/9/4/2/942b2336ccb4cf42b2cbd07ed9c75ede.png) , b)
, b) ![\left ( \sqrt[3]{a^2} \right )^6](/wikipedia/images/math/9/a/1/9a1db4aea08869857d67618e54707551.png) , c)
, c) ![\sqrt{\sqrt[3]{a}}](/wikipedia/images/math/4/7/3/473cf1ea29276b3cfe84680bf3548a10.png) , d)
, d) ![\sqrt[3]{3} \cdot \sqrt[3]{9}](/wikipedia/images/math/6/d/2/6d24beca08bdb942089cf6ad8b4c7d1c.png) , e)
, e) 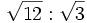
a) ![\sqrt[12]{x^9}=\sqrt[4 \cdot 3]{x^{3 \cdot 3}}=\sqrt[4]{x^{3}}](/wikipedia/images/math/d/1/9/d190b659acadff5f242846e5d6014e10.png) , usando la propiedad nº 1.
, usando la propiedad nº 1.
b) ![\left ( \sqrt[3]{a^2} \right )^6=\sqrt[3]{a^{12}}=a^{\frac{12}{3}}=a^4](/wikipedia/images/math/9/4/b/94b477fe13f98eac4d76261cf2c34d2c.png) , usando la propiedad nº 2 y transformando el radical en potencia de exponente fraccionario.
, usando la propiedad nº 2 y transformando el radical en potencia de exponente fraccionario.
c) ![\sqrt{\sqrt[3]{a}}=\sqrt[2 \cdot 3]{a}=\sqrt[6]{a}](/wikipedia/images/math/9/4/a/94ad123ac81d4cf1d017be5a726de942.png) , usando la propiedad nº 3.
, usando la propiedad nº 3.
d) ![\sqrt[3]{3} \cdot \sqrt[3]{9}= \sqrt[3]{3 \cdot 9} =\sqrt[3]{27}=3](/wikipedia/images/math/b/7/b/b7b21e3525e1caa80c30fe91bbb85c77.png) , usando la propiedad nº 4.
, usando la propiedad nº 4.
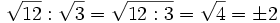 , usando la propiedad nº 5.
, usando la propiedad nº 5.Pulsa el botón EJERCICIO y verás el enunciado; hazlo en tu cuaderno e introduce la solución con la escena, luego pulsa el botón SOLUCIÓN para ver si lo has hecho bien.
Propiedades de las operaciones con radicales. Ejemplos.
Simplifica: 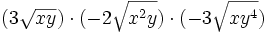
Simplifica: ![(-8\sqrt[3] {x^{10}y^2}) : (-4\sqrt[3] {xy^{11}})](/wikipedia/images/math/2/1/b/21b675f2e891ca1cd137acdf888cbcde.png)
Calcula: ![\sqrt[4]{\cfrac{81}{16}}](/wikipedia/images/math/9/e/d/9ed2bdc3b33dce510e788cce2d6938b7.png)
Calcula:
1) 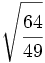 2)
2) ![\sqrt[4]{\cfrac{1}{81}}](/wikipedia/images/math/a/5/4/a54618bf9ee77a830fab9a825f43fad0.png) 3)
3) ![\sqrt[3]{\cfrac{-27~~}{125}}](/wikipedia/images/math/5/c/3/5c3b48c07709122b11aadf157c159924.png) 4)
4) ![\sqrt[5]{\cfrac{-32~~}{243}}](/wikipedia/images/math/7/5/8/758e101bb00fde536dd8dc589f2eab1d.png)
Suma y resta de radicales semejantes
Para sumar y restar radicales, éstos deben ser semejantes, es decir, tener el mismo radicando y el mismo índice. En tal caso el radical el radical resultante tiene como coeficiente la suma o resta de los coeficientes de cada uno de los radicales.
Ejemplo: Suma y resta de radicales con el mismo índice y radicando
Efectúa las siguientes sumas y restas de radicales:
1. 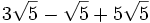
2. 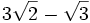
3. ![3\sqrt[3]{2}+\sqrt{2}](/wikipedia/images/math/f/5/5/f554a76b3698de9bd3d86d6600364c25.png)
1. 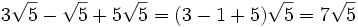
2. 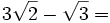 (No se puede simplificar)
(No se puede simplificar)
![3\sqrt[3]{2}+\sqrt{2}=](/wikipedia/images/math/a/6/e/a6edb4be927bfe44dff1ae00ac0eb772.png) (No se puede simplificar)
(No se puede simplificar)Suma y resta de radicales semejantes. Ejemplos.
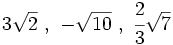
![3\sqrt[3]{2} \ , \ -\sqrt[3]{2} \ , \ \cfrac{2}{3}\sqrt[3]{2}](/wikipedia/images/math/1/1/c/11ca38664b260e771d7b6b60dd01d52b.png)

