Plantilla:Ecuaciones de segundo grado incompletas
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 18:42 1 jun 2017 Coordinador (Discusión | contribuciones) (→Ecuaciones de segundo grado incompletas) ← Ir a diferencia anterior |
Revisión de 10:34 6 jun 2017 Coordinador (Discusión | contribuciones) (→Ecuaciones de segundo grado incompletas) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | ==Ecuaciones de segundo grado incompletas== | + | ===Ecuaciones de segundo grado incompletas=== |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| Una ecuación de segundo grado, {{sube|porcentaje=17%|contenido=<math>ax^2+bx+c=0\;\!</math>}}, es incompleta, si {{sube|porcentaje=17%|contenido=<math>b=0\;</math>}} ó {{sube|porcentaje=17%|contenido=<math>c=0\;</math>}}: | Una ecuación de segundo grado, {{sube|porcentaje=17%|contenido=<math>ax^2+bx+c=0\;\!</math>}}, es incompleta, si {{sube|porcentaje=17%|contenido=<math>b=0\;</math>}} ó {{sube|porcentaje=17%|contenido=<math>c=0\;</math>}}: | ||
Revisión de 10:34 6 jun 2017
Ecuaciones de segundo grado incompletas
Una ecuación de segundo grado, 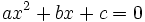 , es incompleta, si
, es incompleta, si 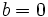 ó
ó 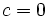 :
:
- Si
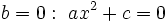
- Si
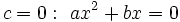
Resolución de las ecuaciones de segundo grado incompletas
- En el caso
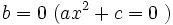 , las soluciones se obtienen despejando x:
, las soluciones se obtienen despejando x:
- En el caso
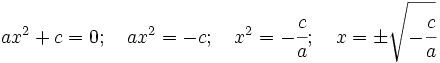
- En el caso
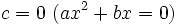 , las soluciones se obtienen sacando factor común e igualando a cero cada factor:
, las soluciones se obtienen sacando factor común e igualando a cero cada factor:
- En el caso
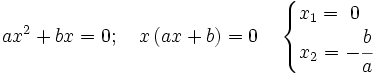
En la escena, pulsa "INICIO" para ver otros ejemplos.
En la escena, pulsa "INICIO" para ver otros ejemplos.
Ecuaciones de segundo grado sin termino lineal. Ejemplos.
Ecuaciones de segundo grado sin termino independiente. Ejemplos.

