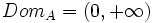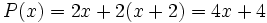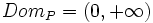Plantilla:Expresión analítica de una función
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 08:33 4 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 08:33 4 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 44: | Línea 44: | ||
| }} | }} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Problema 1 | + | |titulo1=Ejercicio 1 |
| |duracion=7'14" | |duracion=7'14" | ||
| |sinopsis=Se va a construir una caja rectangular sin tapa a partir de una lámina metálica de 30 cm de largo por 20 cm de ancho. Para ello se van a recortar cuadrados de lado "x" en las esquinas y luego se van a doblar los lados hacia arriba. Obtén la expresión analítica que relaciona el volumen "V" de la caja en función del lado "x". | |sinopsis=Se va a construir una caja rectangular sin tapa a partir de una lámina metálica de 30 cm de largo por 20 cm de ancho. Para ello se van a recortar cuadrados de lado "x" en las esquinas y luego se van a doblar los lados hacia arriba. Obtén la expresión analítica que relaciona el volumen "V" de la caja en función del lado "x". | ||
| Línea 51: | Línea 51: | ||
| {{p}} | {{p}} | ||
| {{Video_enlace_julioprofe | {{Video_enlace_julioprofe | ||
| - | |titulo1=Problema 2 | + | |titulo1=Ejercicio 2 |
| |duracion=9'07" | |duracion=9'07" | ||
| |sinopsis=Expresa el área "A" de un triángulo equilátero en función de sus lado "L". | |sinopsis=Expresa el área "A" de un triángulo equilátero en función de sus lado "L". | ||
| |url1=https://www.youtube.com/watch?v=25VPnBQD3LA | |url1=https://www.youtube.com/watch?v=25VPnBQD3LA | ||
| + | }} | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión de 08:33 4 jun 2017
La expresión analítica de una función es una ecuación que relaciona la variable dependiente con la variable independiente.
Ejemplo: Expresión analítica de una función
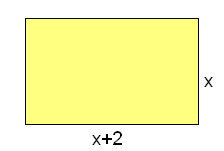
Un rectángulo mide 2 cm más de largo que de ancho.
- Halla la expresión analítica de la función que relaciona su área con su lado menor. Halla su dominio.
- Halla la expresión analítica de la función que relaciona su perímetro con su lado menor. Halla su dominio.
- Haz una tabla de valores para cada función.
- Representa gráficamente las dos funciones anteriores.
Solución:
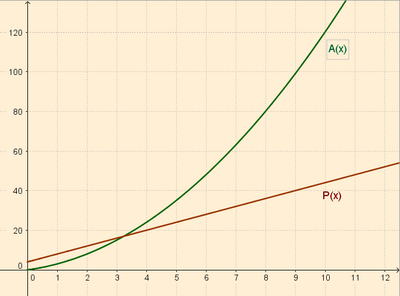
3. Tablas de valores:
4. Representación gráfica: A partir de los valores de las tablas anteriores, dibujamos los puntos de las gráficas: la dell área (en verde) y la del perímetro (en marrón).
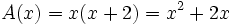
 , no puede ser un número negativo, su dominio es:
, no puede ser un número negativo, su dominio es: