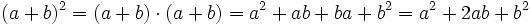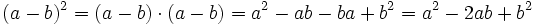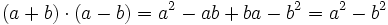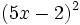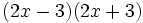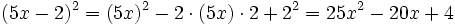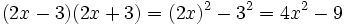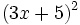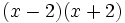Plantilla:Identidades notables
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 05:58 13 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 06:03 13 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 176: | Línea 176: | ||
| |url1=https://www.youtube.com/watch?v=H55N3AvsqE0 | |url1=https://www.youtube.com/watch?v=H55N3AvsqE0 | ||
| }} | }} | ||
| - | }} | + | ---- |
| {{Video_enlace_matemovil | {{Video_enlace_matemovil | ||
| - | |titulo1=Problema 1 | + | |titulo1=Eercicio 1 |
| |duracion=8'42" | |duracion=8'42" | ||
| |sinopsis= | |sinopsis= | ||
| Línea 185: | Línea 185: | ||
| b) Sabiendo que <math>\left(a+\cfrac{1}{a}\right)^2=3\;</math>, halla <math>a^3+\cfrac{1}{a^3}\;</math>. | b) Sabiendo que <math>\left(a+\cfrac{1}{a}\right)^2=3\;</math>, halla <math>a^3+\cfrac{1}{a^3}\;</math>. | ||
| |url1=https://www.youtube.com/watch?v=-foE--Iq-tE&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=19 | |url1=https://www.youtube.com/watch?v=-foE--Iq-tE&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=19 | ||
| + | }} | ||
| + | {{Video_enlace_matemovil | ||
| + | |titulo1=Eercicio 2 | ||
| + | |duracion=10'41" | ||
| + | |sinopsis= | ||
| + | a) Efectúa: <math>30001^2-30000^2\;</math>. | ||
| + | |||
| + | b) Halla la sexta potencia de <math>\sqrt{2+\sqrt{3}}+\sqrt{2-\sqrt{3}}</math>. | ||
| + | |||
| + | c) Sabiendo que <math>a+b=\sqrt{5}\;</math> y <math>a \cdot b = 3\;</math>, halla <math>(a-b)^2\;</math>. | ||
| + | |url1=https://www.youtube.com/watch?v=psqPy_6J5bo&list=PL3KGq8pH1bFRmhsCe2sPnUj199NNvQWQZ&index=20 | ||
| + | }} | ||
| + | |||
| }} | }} | ||
| {{wolfram desplegable|titulo=Productos notables|contenido= | {{wolfram desplegable|titulo=Productos notables|contenido= | ||
Revisión de 06:03 13 jun 2017
Productos notables
- Cuadrado de una suma:
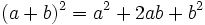
- Cuadrado de una diferencia:

- Suma por diferencia:
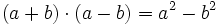
Demostración:
- Cuadrado de una suma:
Escena que demuestra geométricamente la fórmula del cuadrado de una suma
- Cuadrado de una diferencia:
Escena que demuestra geométricamente la fórmula del cuadrado de una diferencia
- Suma por diferencia:
Escena que demuestra geométricamente la fórmula de la suma por diferencia
Productos notables. Ejemplos.
- Fórmulas del cuadrado de una suma y de una diferencia.
- Ejemplos::
- a)

- b)
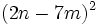
- Fórmula de la suma por diferencia.
- Ejemplos:
- a)
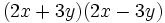
- b)
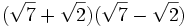
- c)
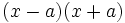
Desarrolla:
- a)
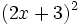
- b)
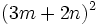
- c)
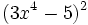
- d)
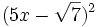
Desarrolla:
- a)
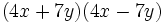
- b)
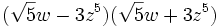
- c)

Desarrolla: 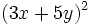
Desarrolla: 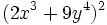
Desarrolla: 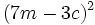
Desarrolla: 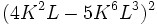
Desarrolla: 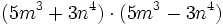
Desarrolla:
a) 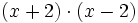
b) 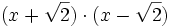
c) 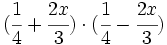
d) 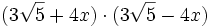
e) 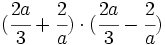
- Cubo de una suma:
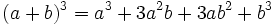
- Cubo de una diferencia:
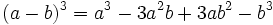
- Ejemplos.
- Suma de cubos:
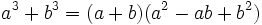
- Diferencia de cubos:
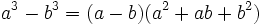
- Ejemplos.
- Cuadrado de un trinomio:
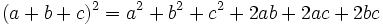
- Ejemplos.
a) Sabiendo que 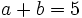 y
y 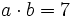 , halla
, halla 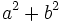 .
.
b) Sabiendo que 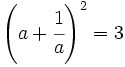 , halla
, halla 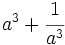 .
.
a) Efectúa: 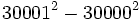 .
.
b) Halla la sexta potencia de 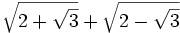 .
.
c) Sabiendo que 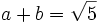 y
y 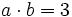 , halla
, halla 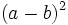 .
.