Plantilla:Límites infinitos
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:24 21 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 18:57 17 abr 2018 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 6: | Línea 6: | ||
| <center><math>\lim_{x \to a^-} f(x)=+\infty</math></center> | <center><math>\lim_{x \to a^-} f(x)=+\infty</math></center> | ||
| {{p}} | {{p}} | ||
| - | *Una función <math>f(x)\;</math> tiende a <math>+\infty</math> por la derecha de un punto <math>c\;</math>, si <math>f(x)\;</math> se aproxima a valores positivos cada vez más grandes y no acotables, cuando <math>x \rightarrow c^+\;</math>. Lo representaremos: | + | *Una función <math>f(x)\;</math> tiende a <math>+\infty</math> por la derecha de un punto <math>a\;</math>, si <math>f(x)\;</math> se aproxima a valores positivos cada vez más grandes y no acotables, cuando <math>x \rightarrow a^+\;</math>. Lo representaremos: |
| - | <center><math>\lim_{x \to c^+} f(x)=+\infty</math></center> | + | <center><math>\lim_{x \to a^+} f(x)=+\infty</math></center> |
| {{p}} | {{p}} | ||
| *Una función <math>f(x)\;</math> tiende a <math>+\infty</math> en un punto <math>c\;</math>, si | *Una función <math>f(x)\;</math> tiende a <math>+\infty</math> en un punto <math>c\;</math>, si | ||
Revisión de 18:57 17 abr 2018
El concepto de límite visto en el apartado anterior puede extenderese al caso en que, al aproximarnos al punto 
, la función se aproxime a 
ó 
.
- Una función
tiende a por la izquierda de un punto , si se aproxima a valores positivos cada vez más grandes y no acotables, cuando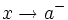 
. Lo representaremos:
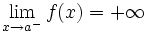
- Una función tiende a por la derecha de un punto , si se aproxima a valores positivos cada vez más grandes y no acotables, cuando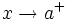
. Lo representaremos:
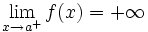
- Una función tiende a en un punto
, si
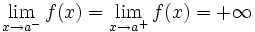
y lo representaremos:
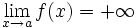
- De forma análoga se puede definir la tendencia a si cambiamos la frase "se aproxima a valores positivos cada vez más grandes y no acotables" por "se aproxima a valores negativos cada vez más pequeños y no acotables", en los tres casos.
- En todos estos casos diremos que la función tiene una asíntota vertical en el punto
.
Límites infinitos (14'32") Sinopsis: En este vídeo definimos el concepto de límite infinito de una función en un punto y lo interpretamos geométricamente: asíntotas verticales.
