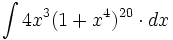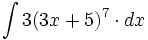Cálculo de primitivas inmediatas (2ºBach)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:26 25 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:34 25 jun 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 17: | Línea 17: | ||
| |enunciado=:Primitivas del tipo <math>\int [u(x)]^m \cdot u'(x) \cdot dx \quad m \ne -1</math> | |enunciado=:Primitivas del tipo <math>\int [u(x)]^m \cdot u'(x) \cdot dx \quad m \ne -1</math> | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
| - | |titulo1=1. Ejemplo | + | |titulo1=Ejercicio 1 |
| - | |duracion=9'19" | + | |duracion=7'01" |
| |sinopsis= | |sinopsis= | ||
| - | |url1=http://www.matematicasbachiller.com/videos/cintegral/01/in01_05a1_media/in01_05a1.wmv | + | #<math>\int 4x^3(1+x^4)^{20} \cdot dx</math> |
| + | #<math>\int 3(3x+5)^7 \cdot dx</math> | ||
| + | |||
| + | |url1=https://www.youtube.com/watch?v=N4yIQcm-8zY&list=PLECA0C7A8B59E5534&index=5 | ||
| }} | }} | ||
| {{Video_enlace2 | {{Video_enlace2 | ||
Revisión de 10:34 25 jun 2017
Menú:
| Enlaces internos | Para repasar o ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Ejemplos: Primitivas inmediatas
- Primitivas del tipo
![\int [u(x)]^m \cdot u'(x) \cdot dx \quad m \ne -1](/wikipedia/images/math/2/0/0/200687db4a9a936cd627487814a1fad2.png)
Ejemplos: Primitivas inmediatas
Ejemplos: Primitivas inmediatas
Ejemplos: Primitivas inmediatas
Ejemplos: Primitivas inmediatas
Ejemplos: Primitivas inmediatas
Ejemplos: Primitivas inmediatas
Ejemplos: Primitivas inmediatas
- Primitivas del tipo
![\int \cfrac{u'(x)}{a^2+[u(x)]^2} \cdot dx](/wikipedia/images/math/1/2/1/1216aad7e7c8189456878755ca0c846c.png)
Ejemplos: Primitivas inmediatas
- Primitivas del tipo
![\int \cfrac{u'(x)}{\sqrt{a^2-[u(x)]^2}} \cdot dx](/wikipedia/images/math/7/0/e/70e26d7ca7ea8762b35e39fea301f6a4.png)