Aplicaciones de la derivada (2ºBach)

De Wikipedia

(Diferencia entre revisiones)

Revisión de 08:40 27 jun 2017

Menú:

Enlaces internos	Para repasar o ampliar	Enlaces externos
Indice Descartes Manual Casio		WIRIS Calculadora

Tabla de contenidos

1 Estudio del crecimiento y de los puntos singulares
2 Utilidad de la segunda derivada
3 Teoremas de Rolle, Lagrange y Cauchy
4 Ejercicios

Estudio del crecimiento y de los puntos singulares

Procedimiento

Para estudiar el crecimiento de una función deberemos estudiar el signo de la función derivada:

En aquellos puntos donde la derivada sea positiva la función será creciente.
En aquellos puntos donde la derivada sea negativa la función será decreciente.

Estudio del crecimiento

Tutorial 1a (13'02") Sinopsis:

Funciones crecientes y decrecientes

Tutorial 1b (7'19") Sinopsis:

Criterios de crecimiento y decrecimiento

Ejercicio 1a (2'55") Sinopsis:

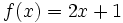
Estudia el crecimiento de $f(x)=2x+1\;$

Ejercicio 1b (4'01") Sinopsis:

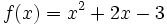
Estudia el crecimiento de $f(x)=x^2+2x-3\;$

Ejercicio 1c (8'31") Sinopsis:

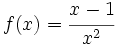
Estudia el crecimiento de $f(x)=\cfrac{x-1}{x^2}\;$

Ejercicio 2 (3'10") Sinopsis:

Demuestra que 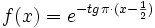$f(x)=e^{-tg \, \pi \cdot (x-\frac{1}{2})}$ es positiva y decreciente en el intervalo (0,1).

Se llaman puntos singulares de una función a los puntos en los que la derivada vale cero. Son puntos de tangente horizontal.

Esos puntos pueden ser puntos extremos (máximos o mínimos), pero también pueden no serlo. Para determinar qué son, deberemos estudiar el crecimiento de la función.

Extremos de una función

Tutorial 1a (11'58") Sinopsis:

Monotonía y extremos relativos

Tutorial 1b (17'13") Sinopsis:

Monotonía y extremos relativos.Ejemplos

Tutorial 2 (23'32") Sinopsis:

¿Qué son los puntos máximos, mínimos, locales y globales, crecimiento y decrecimiento?

Tutorial 3a (13'46") Sinopsis:

Determinación de los extremos relativos

Tutorial 3b (14'45") Sinopsis:

Determinación de máximos y mínimos absolutos

Ejercicio 1 (9'04") Sinopsis:

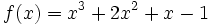
Estudia el crecimiento y los puntos extremos de $f(x)=x^3+2x^2+x-1\;$

Ejercicio 2a (13'12") Sinopsis:

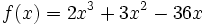
Estudia el crecimiento y los puntos extremos de $f(x)=2x^3+3x^2-36x\;$

Ejercicio 2b (11'57") Sinopsis:

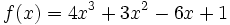
Estudia el crecimiento y los puntos extremos de $f(x)=4x^3+3x^2-6x+1\;$

Ejercicio 2c (11'34") Sinopsis:

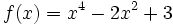
Estudia el crecimiento y los puntos extremos de $f(x)=x^4-2x^2+3\;$

Ejercicio 2d (6'49") Sinopsis:

Halla los máximos y mínimos de 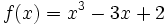$f(x)=x^3-3x+2\;$

Ejercicio 2e (7'42") Sinopsis:

Encuentra el valor de "k" tal que 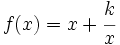$f(x)=x+\cfrac{k}{x}\;$ tenga un máximo local en x=-2.

Ejercicio 3a (4'58") Sinopsis:

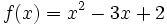
Halla los máximos y mínimos de $f(x)=x^2-3x+2\;$

Ejercicio 3b (8'11") Sinopsis:

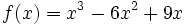
Halla los máximos y mínimos de $f(x)=x^3-6x^2+9x\;$

Ejercicio 3c (9'43") Sinopsis:

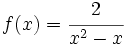
Halla los máximos y mínimos de $f(x)=\cfrac{2}{x^2-x}\;$

Ejercicio 3d (7'52") Sinopsis:

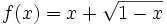
Halla los máximos y mínimos de $f(x)=x+\sqrt{1-x}\;$

Ejercicio 3e (7'02") Sinopsis:

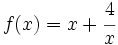
Halla los máximos y mínimos de $f(x)=x+\cfrac{4}{x}\;$

Ejercicio resuelto: Puntos singulares y crecimiento

Dada la función 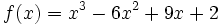$f(x)=x^3-6x^2+9x+2\;$ , halla sus puntos singulares y estudia su crecimiento.

Solución:

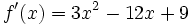
$f'(x)=3x^2-12x+9\;$

Puntos singulares:

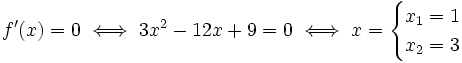
$f'(x)=0 \iff 3x^2-12x+9=0 \iff x=\begin{cases} x_1= 1 \\ x_2=3 \end{cases}$

Para estudiar el crecimiento determinaremos el signo de la función derivada mediante una tabla en la que estableceremos zonas delimitadas por los puntos singulares y por los puntos de discontinuidad, si los hubiese. En nuestro caso hay 3 zonas porque hay 2 puntos singulares y no hay discontinuidades, por tratarse f'(x) de una función polinómica.

             -inf     1       3    +inf       
          -----!------!-------!------!
          f'(x)!  +   !   -   !  +   !
          -----!------!-------!------!
           f(x)! Cre  ! Decre ! Cre  !
          ----------------------------

Como f(1)=6 y f(3)=2, el anterior análisis del crecimiento nos permite determinar que (1,6) es un máximo y (3,2) es un mínimo.

Extremos relativos

Actividad: Extremos relativos

Nota para los cursos de secundaria: Algunas de las siguientes actividades son sólo ilustrativas ya que su resolución manual requiere conocimientos de 1º de bachillerato.

a) Halla los máximos relativos de la función $y=x(40-x)\;$

b) Halla los mínimos relativos de la función $y=x^2+2x+1\;$

c) Halla los extremos relativos (máximos y mínimos relativos) de la función $y=\cfrac{x^3}{3}-x^2-8x\;$ .

Solución:

Para averiguar las soluciones debes escribir donde pone "Escribe tu consulta" las siguientes expresiones:

a) maxima x(40-x)

b) minima x^2+2x+1

c) extrema x^3/3-x^2-8x

Utilidad de la segunda derivada

Derivadas de orden superior (16'51") Sinopsis:

Utilidad de la segunda derivada

Concavidad y puntos de inflexión (30'41") Sinopsis:

Concavidad:

Ejercicio 1 (2'44") Sinopsis:

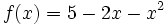Estudia la concavidad de $f(x)=5-2x-x^2\;$ .

Ejercicio 2 (5'20") Sinopsis:

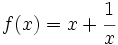Estudia la concavidad de $f(x)=x+\cfrac{1}{x}$ .

Ejercicio 3 (8'28") Sinopsis:

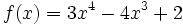Estudia la concavidad de $f(x)=3x^4-4x^3+2\;$ .

Puntos de inflexión:

Ejercicio 1 (4'07") Sinopsis:

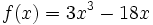Estudia la concavidad de $f(x)=3x^3-18x\;$ .

Ejercicio 2 (11'24") Sinopsis:

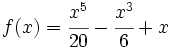Estudia la concavidad de $f(x)=\cfrac{x^5}{20}-\cfrac{x^3}{6}+x$ .

Ejercicio 3 (7'02") Sinopsis:

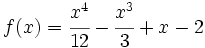Estudia la concavidad de $f(x)=\cfrac{x^4}{12}-\cfrac{x^3}{3}+x-2$ .

Ejercicio 4 (7'30") Sinopsis:

Hallar "a", "b" y "c" para que la función 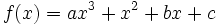$f(x)=ax^3+x^2+bx+c\;$ tenga un máximo relativo en (0,3) y un punto de inflexión en x=1.

Máximos y mínimos (usando f "):

Ejercicio 1 (5'16") Sinopsis:

Estudia los máximos y mínimos de 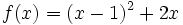$f(x)=(x-1)^2+2x\;$ .

Ejercicio 2 (9'04") Sinopsis:

Estudia los máximos y mínimos de No se pudo entender (función desconocida\cfac): f(x)=\cfac{1}{3}x^3-x\; .

Ejercicio 3 (8'59") Sinopsis:

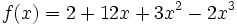Estudia los máximos y mínimos de $f(x)=2+12x+3x^2-2x^3\;$ .

Ejercicio 4 (5'33") Sinopsis:

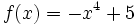Estudia los máximos y mínimos de $f(x)=-x^4+5\;$ .

Ejercicio 5 (16'49") Sinopsis:

Estudia los máximos y mínimos de No se pudo entender (función desconocida\cfac): f(x)=\cfac{x^2-3}{x^3}\; .

Teoremas de Rolle, Lagrange y Cauchy

Teorema de Rolle. Teorema de Lagrange (20'03") Sinopsis:

00.00 - Introducción.
05:15 - Teorema de Rolle.
13:00 - Teorema de Lagrange.

Teorema de Cauchy (9'29") Sinopsis:

Una generalización del teorema de Lagrange.

Ejercicio 1 (2'35") Sinopsis:

Prueba que f(x)=

Ejercicio 2 (4'29") Sinopsis:

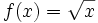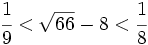Aplicando el teorema de Lagrange a $f(x)= \sqrt{x}\;$ , demostrar que $\cfrac{1}{9} < \sqrt{66} - 8 < \cfrac{1}{8}$ .

Ejercicio 3 (1'51") Si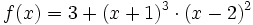nopsis:

Si $f(x)= 3+(x+1)^3 \cdot (x-2)^2\;$ , ¿tiene f'(x)=0 alguna solución en el intervalo (-1,2)?

Ejercicio 4 (2'51") Sinopsis:

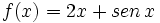Comprueba si $f:[0,2\pi] \rightarrow \mathbb{R}$ , tal que $f(x)= 2x+sen \, x\;$ cumple las hipótesis del teorema de Lagrange, y determina los puntos a los que hace referencia dicho teorema.

Ejercicios

Problema (4'18") Sinopsis:

Si el lado de un cuadrado aumenta a una velocidad constante de 3cm/seg, halla la velocidad a la que aumenta el área del cudrado cuando el lado mide 12 cm, y calcula el valor del lado cuando el área crece a 60 cm²/seg.

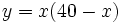
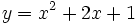
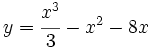Obtenido de "http://maralboran.org/wikipedia/index.php/Aplicaciones_de_la_derivada_%282%C2%BABach%29"

Categorías: Matemáticas | Funciones

 {{Utilidad de la segunda derivada}}
 {{p}}
+==Teoremas de Rolle, Lagrange y Cauchy==
+{{Video_enlace_fonemato
+|titulo1=Teorema de Rolle. Teorema de Lagrange
+|duracion=20'03"
+|sinopsis=
+*00.00 - Introducción.
+*05:15 - Teorema de Rolle.
+*13:00 - Teorema de Lagrange.
+|url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/25-teorema-de-rolle-teorema-de-lagrange-2
+}}
+{{Video_enlace_fonemato
+|titulo1=Teorema de Cauchy
+|duracion=9'29"
+|sinopsis=Una generalización del teorema de Lagrange.
+|url1=https://matematicasbachiller.com/videos/2-bachillerato/introduccion-al-calculo-diferencial-de-una-variable/04-derivabilidad-de-funciones-2/26-teorema-de-cauchy-2
+}}
+{{Video_enlace_fonemato
+|titulo1=Ejercicio 1
+|duracion=2'35"
+|sinopsis=Prueba que f(x)=|x-1| no verifica el teorema de Rolle en el intervalo [-2,0].
+|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/002-ejercicio-7
+}}
+{{Video_enlace_fonemato
+|titulo1=Ejercicio 2
+|duracion=4'29"
+|sinopsis=Aplicando el teorema de Lagrange a <math>f(x)= \sqrt{x}\;</math>, demostrar que <math>\cfrac{1}{9} < \sqrt{66} - 8 < \cfrac{1}{8}</math>.
+|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/003-ejercicio-7
+}}
+{{Video_enlace_fonemato
+|titulo1=Ejercicio 3
+|duracion=1'51"
+|sinopsis=Si <math>f(x)= 3+(x+1)^3 \cdot (x-2)^2\;</math>, ¿tiene f'(x)=0 alguna solución en el intervalo (-1,2)?
+|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/013-ejercicio-6
+}}
+{{Video_enlace_fonemato
+|titulo1=Ejercicio 4
+|duracion=2'51"
+|sinopsis=Comprueba si <math>f:[0,2\pi] \rightarrow \mathbb{R}</math>, tal que <math>f(x)= 2x+sen \, x\;</math> cumple las hipótesis del teorema de Lagrange, y determina los puntos a los que hace referencia dicho teorema.
+|url1=https://matematicasbachiller.com/videos/2-bachillerato/prueba-de-acceso-a-la-universidad-problemas-de-examen/07-teoremas-de-rolle-lagrange-y-cauchy/019-ejercicio-4
+}}
 ==Ejercicios==
 {{Ejercicios: aplicacion derivada}}
 {{p}}
 [[Categoría: Matemáticas]][[Categoría: Funciones]]

Aplicaciones de la derivada (2ºBach)

De Wikipedia

Revisión de 08:40 27 jun 2017

Tabla de contenidos

Estudio del crecimiento y de los puntos singulares

Utilidad de la segunda derivada

Teoremas de Rolle, Lagrange y Cauchy

Ejercicios

Vistas

Herramientas personales

Menú

Buscar

Herramientas