Plantilla:Razones trigonométricas de algunos ángulos importantes
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:25 29 jun 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:21 16 dic 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 39: | Línea 39: | ||
| {{Geogebra_enlace | {{Geogebra_enlace | ||
| |descripcion=En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de 30º, 45º y 60º con valores exactos. | |descripcion=En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de 30º, 45º y 60º con valores exactos. | ||
| - | |enlace=[https://ggbm.at/QXUgkgbK Razones trigonométricas de 30º, 45º y 60º] | + | |enlace=[http://ggbm.at/QXUgkgbK Razones trigonométricas de 30º, 45º y 60º] |
| }} | }} | ||
| - | {{p}} | + | {{Videotutoriales|titulo=Razones trigonométricas de algunos ángulos importantes|enunciado= |
| {{Video_enlace_fonemato | {{Video_enlace_fonemato | ||
| |titulo1=Razones trigonométricas de ángulos complementarios | |titulo1=Razones trigonométricas de ángulos complementarios | ||
| Línea 67: | Línea 67: | ||
| |duracion=3´50" | |duracion=3´50" | ||
| |url1=https://www.youtube.com/watch?v=t5m2HBVF_uw | |url1=https://www.youtube.com/watch?v=t5m2HBVF_uw | ||
| - | |sinopsis=Una regla mnemotécnica para obtener las razones trigonométricas de 0º, 30º, 45º, 60º y 90º }} | + | |sinopsis=Una regla mnemotécnica para obtener las razones trigonométricas de 0º, 30º, 45º, 60º y 90º |
| + | }} | ||
| + | }} | ||
Revisión de 07:21 16 dic 2017
A continuación las razones trigonométricas de algunos ángulos que es conveniente recordar:
| Grados | sen | cos | tg | cosec | sec | cot |
|---|---|---|---|---|---|---|
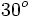
| 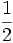
| 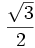
| 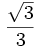
| 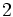
| 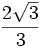
| 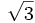
|
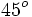
| 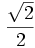
| 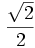
| 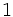
| 
| 
| 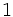
|
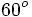
| 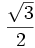
| 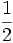
| 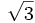
| 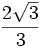
| 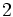
| 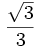
|
En esta escena de Geogebra podrás ver como se calculan las razones trigonométricas de 30º, 45º y 60º con valores exactos.
- Dos ángulos agudos se dicen complementarios si suman 90º.
- El seno de un ángulo agudo coincide con el coseno de su complementario.
- La tangente de un ángulo agudo coincide con la cotangente de su complementario.
- La secante de un ángulo agudo coincide con la cesecante de su complementario.
- Apoyándonos en un triángulo equilátero de lado unidad, en este vídeo determinamos las razones trigonométricas de los ángulos de 30º y 60º.
- También determinamos las razones trigonométricas del ángulo de 45º; para ello nos servimos de un triángulo rectángulo de catetos unitarios.
- Las razones trigonométricas en cuestión deben memorizarse.
Una regla mnemotécnica para obtener las razones trigonométricas de 0º, 30º, 45º, 60º y 90º

