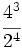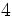Operaciones con potencias (1ºESO)
De Wikipedia
| Revisión de 09:19 1 jul 2017 Coordinador (Discusión | contribuciones) (→Propiedades de las potencias de números naturales) ← Ir a diferencia anterior |
Revisión de 09:45 1 jul 2017 Coordinador (Discusión | contribuciones) (→Actividades) Ir a siguiente diferencia → |
||
| Línea 20: | Línea 20: | ||
| {{Videos: propiedades potencias naturales}} | {{Videos: propiedades potencias naturales}} | ||
| {{p}} | {{p}} | ||
| + | |||
| + | ==Calculadora== | ||
| + | {{Casio FX-100MS: Potencias}} | ||
| ==Actividades== | ==Actividades== | ||
Revisión de 09:45 1 jul 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
(Pág. 31)
Propiedades de las potencias de números naturales
Propiedades de las potencias
- 1. Producto de potencias de la misma base:
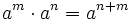
- 2. Cociente de potencias de la misma base:
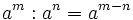
- 3. Potencia de un producto:
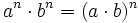
- 4. Potencia de un cociente:
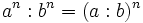
- 5. Potencia de otra potencia:
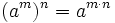
- Producto de potencias de la misma base:
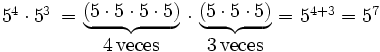
- Cociente de potencias de la misma base:
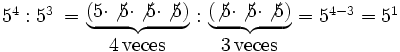
- Potencia de un producto:
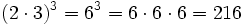
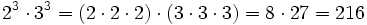
- Potencia de un cociente:
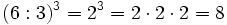
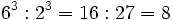
- Potencia de otra potencia:
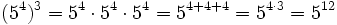
- Potencia cero: Cuando se vio la definición de potencia, dijimos que
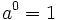 por convenio. Expliquemos ésto ahora un poco mejor:
por convenio. Expliquemos ésto ahora un poco mejor:
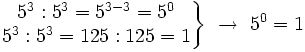
Practica con las propiedades de las operaciones con potencias de números naturales.
Potencias de números naturales con exponente natural.
- Producto de potencias de la misma base.
- Cociente de potencias de la misma base.
- Potencia de otra potencia.
- Ejemplos.
Aprende a multiplicar potencias con la misma base.
Aprende a dividir potencias con la misma base.
Aprende a calcular la potencia de otra potencia.
Aprende a multiplicar potencias con la misma base.
Aprende a dividir potencias con la misma base.
Aprende a calcular la potencia de un producto.
Aprende a calcular la potencia de un cociente.
Aprende a calcular la potencia de una potencia.
Enunciados de las propiedades de las potencias de números naturales.
Ejemplos de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Ejercicio de aplicación de las propiedades de las potencias de números naturales.
Calculadora
|
Calculadora: Potencias |
Actividades
(Pág. 31-32)
Ejercicios resueltos: Operaciones con potencias
- a) Calcula por el camino más sencillo:
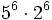
- b) Calcula por el camino más sencillo:
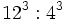
- c) Calcula con la ayuda de las propiedades:
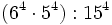
- d) Calcula con la ayuda de las propiedades:
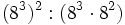
- e) Reduce a una sola potencia:
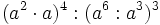
- a) Aplicando la propiedad 3:
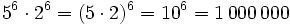
- b) Aplicando la propiedad 4:
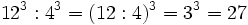
- c) Aplicando la propiedad 3:
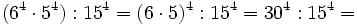
- y aplicando la propiedad 4:
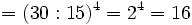
- d) Aplicando las propiedades 5 y 1:
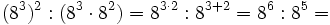
- y aplicando la propiedad 2:
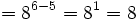
- e) Por las propiedades 1 y 2:
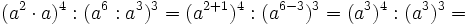
- y por las propiedades 5 y 2:
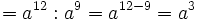
Ejercicios propuestos
|
Ejercicios propuestos: Operaciones con potencias |