Ángulos (1º ESO)
De Wikipedia
| Revisión de 17:07 4 jul 2017 Coordinador (Discusión | contribuciones) (→Relaciones entre ángulos) ← Ir a diferencia anterior |
Revisión de 17:22 4 jul 2017 Coordinador (Discusión | contribuciones) (→Ángulos de lados paralelos) Ir a siguiente diferencia → |
||
| Línea 14: | Línea 14: | ||
| {{Relación entre ángulos}} | {{Relación entre ángulos}} | ||
| {{p}} | {{p}} | ||
| - | ===Ángulos de lados paralelos=== | + | ===Ángulos de lados paralelos o perpendiculares=== |
| - | {{Teorema_sin_demo|titulo=Proposición|enunciado=Dos ángulos cuyos lados son iguales o son iguales o son suplementarios}} | + | {{Teorema_sin_demo|titulo=Proposición|enunciado=*Dos ángulos cuyos lados son paralelos o son iguales o son suplementarios. |
| + | *Dos ángulos cuyos lados son perpendiculares o son iguales o son suplementarios.}} | ||
| {{p}} | {{p}} | ||
| + | |||
| ===Ángulos entre dos paralelas cortadas por una transversal=== | ===Ángulos entre dos paralelas cortadas por una transversal=== | ||
| {{Ángulos entre dos paralelas cortadas por una transversal}} | {{Ángulos entre dos paralelas cortadas por una transversal}} | ||
Revisión de 17:22 4 jul 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Geogebra Calculadora |
Tabla de contenidos |
Ángulos
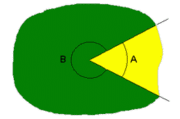
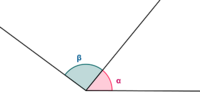
En el dibujo de la derecha puedes ver como dos semirrectas con un origen común determinan siempre dos porciones del plano y por tanto dos ángulos, A y B. Actividad en la que deberás construir un ángulo usando las herramientas de dibujo que se te proporcionan. Ángulos: definición, clasificación y medida. Ángulos: definición, clasificación y medida. Concepto de ángulo. Elementos. Amplitud. Región angular |
Tipos de ángulos
Por su amplitud, distinguimos los siguientes tipos de ángulos:
- Ángulo nulo es aquel definido por dos semirrectas que coinciden. No abarca ninguna porción del plano.
- Ángulo llano es aquel definido por dos semirrectas con la misma dirección, aunque sentidos opuestos. Abarca un semiplano, esto es, la mitad del plano.
- Ángulo convexo es aquel que es menor que un ángulo llano.
- Ángulo cóncavo es aquel que es mayor que un ángulo llano.
- Ángulo recto es aquel ángulo convexo definido por dos semirrectas perpendiculares. Abarca la cuarta parte de un plano.
- Ángulo agudo es aquel que es menor que un ángulo recto.
- Ángulo obtuso es aquel que es mayor que un ángulo recto y menor que un ángulo llano.
- Ángulo completo es aquel que abarca todo el plano.
En esta escena podrás ver una animación con los distintos tipos de ángulos según su abertura.
En este video vamos a ver cómo se clasifican los ángulos según su amplitud: rectos agudos, obtusos, llanos, completos, nulos, convexos y cóncavos.
En este video vamos a clasificar los ángulos según su amplitud de manera dinámica en: nulo, obtuso, llano, cóncavo, convexo, recto y agudo.
En este video vamos a ver la clasificación de los ángulos de acuerdo a sus medidas: ángulo agudo, ángulo recto, ángulo obtuso, ángulo llano, ángulo completo, ángulo entrante o cóncavo, ángulo negativo y ángulo nulo.
Actividad en la que comprobarás tus conocimientos sobre los tipos de ángulos.
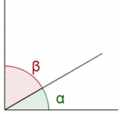
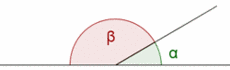
Relaciones entre ángulos
|
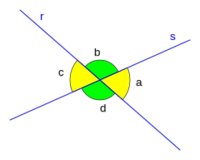
Ángulos complementarios, suplementarios, opuestos por el vértice y formados por rectas secantes.
Con este video vamos a estudiar la clasificación de los ángulos de acuerdo a su relación: ángulos consecutivos, ángulos complementarios, ángulos suplementarios, ángulos conjugados, ángulos opuestos por el vértice y ángulos adyacentes.
Ángulos complementarios y suplementarios. Ejemplos.
Ángulos relacionados según su posición y según su amplitud.
Ángulos consecutivos, complementarios, suplementarios y adyacentes.
Actividad en la que podrás observar las distintas relaciones que hay entre ángulos.
En esta escena podrás interactuar con ángulos complementarios, suplementarios y opuestos por el vértice.
Ángulos de lados paralelos o perpendiculares
Proposición
- Dos ángulos cuyos lados son paralelos o son iguales o son suplementarios.
- Dos ángulos cuyos lados son perpendiculares o son iguales o son suplementarios.
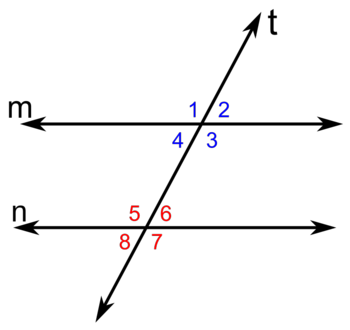
Ángulos entre dos paralelas cortadas por una transversal
Si una recta transversal corta a dos rectas paralelas:
Propiedades
En esta escena podrás ver los distintos tipos de ángulos que se forman al cortar dos rectas paralelas mediante otra recta transversal. También podrás ver cuando estos ángulos coinciden o son suplementarios. |