Plantilla:Triángulo: def y prop
De Wikipedia
| Revisión de 17:56 24 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 09:20 7 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 5: | Línea 5: | ||
| '''Nomenclatura:''' | '''Nomenclatura:''' | ||
| * En un triángulo, la letra que se usa para el vértice es mayúscula: <math>A \,\ B,\ C</math>. Se disponen siguiendo el sentido contrario de las agujas del reloj. | * En un triángulo, la letra que se usa para el vértice es mayúscula: <math>A \,\ B,\ C</math>. Se disponen siguiendo el sentido contrario de las agujas del reloj. | ||
| - | * Las mismas letras mayusculas, con un "sombrero", para nombrar el [[Ángulos (1º ESO)|ángulo]]:<math>\hat A, \ \hat B, \ \hat C</math>, aunque también son usuales las letras griegas: <math>\alpha,\ \beta,\ \gamma</math>. | + | * Las mismas letras mayusculas, con un "sombrero", para nombrar el [[Ángulos (1º ESO)|ángulo]]:<math>\hat A, \ \hat B, \ \hat C</math>, aunque también son usuales las letras griegas: <math>\alpha,\ \beta,\ \gamma</math>. También se puede nombrar un ángulo usando tres vértices. Por ejemplo, <math>\hat{ABC}</math> sería el ángulo <math>\hat B\;</math> |
| * El nombre de cada lado se expresa con una letra minúscula: <math>a,\ b,\ c</math>; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas: <math>BC,\ AC,\ AB</math>, las de los vértices contenidos en ese lado.}} | * El nombre de cada lado se expresa con una letra minúscula: <math>a,\ b,\ c</math>; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas: <math>BC,\ AC,\ AB</math>, las de los vértices contenidos en ese lado.}} | ||
| |celda2=[[Imagen:trinagulo.png|230px]]}} | |celda2=[[Imagen:trinagulo.png|230px]]}} | ||
Revisión de 09:20 7 oct 2017
|
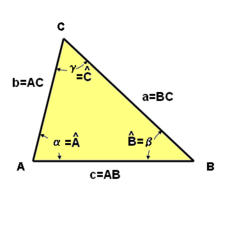
Nomenclatura:
| 
|
Propiedades
Todo triángulo cumple las siguientes propiedades:
- Sus tres ángulo suman 180º.
- La longitud de cada lado es menor que la suma de los otros dos.
- Es rígido, de hecho, es el único polígono indeformable.
- Si
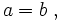 entonces
entonces 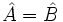 . Y si
. Y si 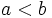 , entonces
, entonces 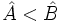 .
.
1. Los tres ángulos de un triángulo suman 180º.
Podrás ver la demostración en el siguiente video:
Demostración de que la suma de los ángulos de un triángulo es un ángulo llano (180º).
Para comprobar esta propiedad vamos a hacer uso de la siguiente escena. En ella, A es un punto fijo, B puede moverse horizontalmente y C libremente: esto permite dibujar cualquier triángulo. La recta que pasa por C es paralela al lado AB con lo cual los ángulos verdes son iguales por ser alternos internos, y los rojos también, por la misma razón. Si sumamos los tres ángulos en el vértice C, obtenemos siempre un ángulo llano.
2. La longitud de cada lado es menor que la suma de los otros dos.
En la siguiente escena puedes comprobar esta propiedad. Mueve los vértices para cambiar la forma del triángulo.
3. Es rígido, de hecho, el triángulo es el único polígono indeformable.
Observa la escena, arrastra los vértices y comprueba que:
a) Con tres varillas iguales podemos formar un triángulo, que no se deforma.
b) Con cuatro varillas iguales, el cuadrilátero que se forma, puede deformarse, no es rígido.
Esta propiedad tiene muchas aplicaciones en la construcción. Observa torres de la luz, estructuras metálicas de puentes,... la forma externa puede ser variada, pero llevan diagonales internas que dividen su estructura en triángulos.Triángulo: Definición, elementos y propiedades
Convenio y notación para nombrar los lados y los ángulos de un triángulo.
Ejercicios de aplicación de la propiedad nº 1 de los triángulos:
"La suma de los ángulos interiores de un triángulo es 180º"
El triángulo es el único polígono rígido.
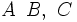 . Se disponen siguiendo el sentido contrario de las agujas del reloj.
. Se disponen siguiendo el sentido contrario de las agujas del reloj.
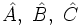 , aunque también son usuales las letras griegas:
, aunque también son usuales las letras griegas: 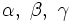 . También se puede nombrar un ángulo usando tres vértices. Por ejemplo,
. También se puede nombrar un ángulo usando tres vértices. Por ejemplo, 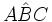 sería el ángulo
sería el ángulo 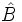
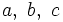 ; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas:
; es la letra correspondiente al vértice opuesto al lado. También se puede expresar cada lado con dos letras mayúsculas: 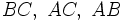 , las de los vértices contenidos en ese lado.
, las de los vértices contenidos en ese lado.

