Plantilla:Función de proporcionalidad directa
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:56 28 jul 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:59 12 dic 2017 Coordinador (Discusión | contribuciones) (→Representación gráfica) Ir a siguiente diferencia → |
||
| Línea 10: | Línea 10: | ||
| {{p}} | {{p}} | ||
| ===Representación gráfica=== | ===Representación gráfica=== | ||
| - | {{Teorema_sin_demo|titulo=Propiedad|enunciado= | + | {{Representación gráfica función proporcionalidad directa}} |
| - | *La gráfica de una función de proporcionalidad directa es una recta que pasa por el origen de coordenadas. | + | |
| - | *En consecuencia, para representarla sólo necesitamos un punto y el origen, los cuales uniremos mediante una línea recta. Para obtener dicho punto usaremos la ecuación. | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
Revisión de 12:59 12 dic 2017
Una función de proporcionalidad directa es aquella cuya expresión analítica puede expresarse como:
 |
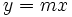es la variable independiente.
es la variable dependiente.
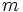una constante que se denomina constante de proporcionalidad o pendiente.
Función de proporcionalidad directa Descripción: En esta escena podrás ver e interactuar con las gráficas de funciones de proporcionalidad directa y estudiar sus propiedades.
Función de proporcionalidad directa Descripción: Definición de función de proporcionalidad directa. Ejemplos.
Representación gráfica
Representación gráfica
- La gráfica de una función de proporcionalidad directa es una recta que pasa por el origen de coordenadas.
- En consecuencia, para representarla sólo necesitamos un punto y el origen, los cuales uniremos mediante una línea recta. Para obtener dicho punto usaremos la ecuación.
Si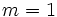 
, la función que se obtiene, 
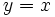, recibe el nombre de función identidad y es la bisectriz del primer y tercer cuadrante.
Ejemplo: Función de proporcionalidad directa
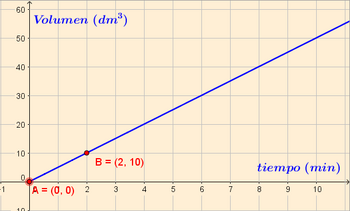
Un grifo, con un caudal de 5 dm3 por minuto, vierte agua en una piscina.
- a) Haz una tabla de valores de la función tiempo-volumen.
- b) Halla la expresión analítica de la función.
- c) Representa gráficamente la función.
Solución:
- a) Tabla de valores:
| tiempo (min) | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Volumen (dm3) | 0 | 5 | 10 | 15 | 20 | 25 | 30 |
- b) Expresión analítica:
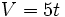(V en dm3; t en minutos)
- c) Representación gráfica: Como se trata de una función de proporcionalidad directa, su gráfica es una recta que pasa por el origen. Por tanto, solo tendremos que representar un punto y el origen, y unirlos mediante una línea recta.
- Sólo se representan los valores
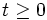, ya que los valores negativos no pertenecen al dominio de esta función.
Actividades en las que aprenderás a representar funciones de proporcionalidad directa y a identificar su ecuación a partir de su gráfica.
