Plantilla:Parámetros estadísticos

De Wikipedia

(Diferencia entre revisiones)
Revisión de 09:03 30 jul 2017
Coordinador (Discusión | contribuciones)
(→Actividades)
← Ir a diferencia anterior		 Revisión de 09:04 30 jul 2017
Coordinador (Discusión | contribuciones)
(→Varianza y desviación típica)
Ir a siguiente diferencia →
Línea 441: Línea 441:
}} }}
{{p}} {{p}}
-{{Videotutoriales|titulo=Cálculo de la vararianza y de la desviación típica|enunciado=+{{Videotutoriales|titulo=Vararianza y desviación típica|enunciado=
{{Video_enlace_tutomate {{Video_enlace_tutomate
|titulo1=Tutorial (caso variable discreta) |titulo1=Tutorial (caso variable discreta)

Revisión de 09:04 30 jul 2017

Tabla de contenidos

Parámetros estadísticos

Después de haber representado los datos gráficamente, ahora llega el momento de hacer un estudio de los mismos. Si estamos estudiando la estatura de todos los alumnos y alumnas del instituto y necesitamos dar información de este estudio, parece lógico dar un dato que conocemos todos como media y que representa la estatura de todo el alumnado estudiado. Además de este dato existen otros datos (que llamaremos parámetros) que van a representar a toda la población o que nos van a informar sobre la población.

Parámetros estadísticos: Son datos que resumen el estudio realizado en la población. Pueden ser de dos tipos:

  • Parámetros de centralización. Son datos que representan de forma global a toda la población. Entre ellos vamos a estudiar la media aritmética, la moda y la mediana.
  • Parámetros de dispersión. Son datos que informan de la concentración o dispersión de los datos respecto de los parámetros de centralización. Por ejemplo el recorrido, la varianza y la desviación típica.

Parámetros de centralización

Moda

Se define la moda como el valor de la variable que más se repite, es el decir, aquél que tiene mayor frecuencia absoluta. Se representa por Mo.

Moda     Descripción:

Actividades en la que podrás aprender a calcular la moda de una distribución estadística.

Moda     Descripción:

Ejemplos con los que podrás aprender a calcular la moda de una distribución estadística.

Autoevaluación: Moda     Descripción:

Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la moda de una distribución estadística.

Actividad: Moda     Descripción:

Calcula en tu cuaderno la moda para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividades:

a) Modifica las frecuencias y observa como puede variar el valor de la moda.

b) ¿Puede una distribución estadística tener más de una moda? ¿Pueden ser todos los valores de la variable?

video
Moda
Tutorial (5´02")     Sinopsis:

Moda correspondiente a una muestra:

  • Definición.
  • Ejemplos.
Ejemplo 1 (datos no agrupados) (4'47")     Sinopsis:

Cálculo de la moda para datos sin agrupar.

Ejemplo 2 (datos agrupados con o sin intervalos) (9'05")     Sinopsis:

Cálculo de la moda para datos agrupados con o sin intervalos.

Media

Se define la media como la suma de todos los datos dividida por el número de datos. Se representa por 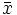\bar x\.

Para calcular la media hacemos:

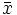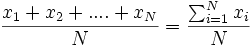
\bar x\ = \frac{x_1 + x_2 + ....+x_N} {N}={\sum_{i=1}^N x_i \over N}

donde 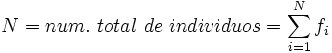N = num.\ total\ de\ individuos = \sum_{i=1}^N f_i.

Sin embargo, podemos observar que aparecen datos repetidos y que en un estudio estadístico tenemos los datos agrupados en una tabla en la que aparecen las frecuencias. Por tanto, podemos simplificar el cálculo de la media aritmética con la fórmula:

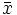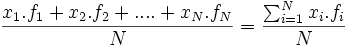
\bar x\ = \frac{x_1.f_1 + x_2.f_2 + ....+x_N.f_N} {N}={\sum_{i=1}^N x_i.f_i \over N}

Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como xi las marcas de clase: los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo.

Media     Descripción:

Actividades en la que podrás aprender a calcular la media de una distribución estadística.

Media (pocos datos)     Descripción:

Ejemplos de cálculo de medias de un conjunto de pocos datos.

Autoevaluación: Media (pocos datos)     Descripción:

Actividades para que practiques el cálculo de medias de un conjunto de pocos datos.

Media (muchos datos)     Descripción:

Ejemplos de cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos.

Autoevaluación: Media (muchos datos)     Descripción:

Actividades para que practiques el cálculo de medias de un conjunto de muchos datos agrupados o no por intervalos.

Actividad 1: Media (Variable discreta)     Descripción:

Calcula en tu cuaderno la media para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividades:

  1. Modifica las frecuencias y observa como puede variar el valor de la media.
  2. ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.
  3. ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.
Actividad 2: Media (Variable continua)     Descripción:

Calcula en tu cuaderno la media para el ejemplo de las estaturas: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, agrupando los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividades:

  1. Modifica las frecuencias y observa como puede variar el valor de la media.
  2. ¿Cuál es el menor valor que puede tomar la media? Justifica la respuesta.
  3. ¿Cuál es el mayor valor que puede tomar la media? Justifica la respuesta.
  4. En este caso, se ha calculado la media utilizando intervalos, pero como tenemos pocos valores de la variable, calcúlala ahora utilizando la definición, es decir, suma todos las estaturas y divide el resultado por el número de alumnos y alumnas que hay. ¿Coincide el resultado? ¿Por qué?

video
Media
Tutorial (7´34")     Sinopsis:

Media aritmética correspondiente a una muestra con datos agrupados o no agrupados.

Ejemplo 1 (datos no agrupados) (7'58")     Sinopsis:

Cálculo de la media para datos no agrupados.

Ejemplo 2 (datos agrupados con o sin intervalos) (16'45")     Sinopsis:

Cálculo de la media para datos agrupados con o sin intervalos.

Mediana

Si ordenamos todos los valores de la variable de menor a mayor, se define la mediana como el valor de la variable que está en el centro. Se representa por Me. Aquí tenemos que comprender que si hay un número impar de valores, habrá un sólo valor central; mientras que si hay un número par de valores habrá dos valores centrales.

Mediana y cuartiles     Descripción:

Actividades en la que podrás aprender a calcular la mediana y los cuartiles primero y tercero de una distribución estadística.

Mediana (pocos datos)     Descripción:

Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística.

Autoevaluación: Mediana (pocos datos)     Descripción:

Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística.

Mediana (muchos datos)     Descripción:

Ejemplos con los que podrás aprender a calcular la mediana de una distribución estadística con muchos datos en tabla de frecuencias.

Autoevaluación: Mediana (muchos datos)     Descripción:

Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la mediana de una distribución estadística con muchos datos en tabla de frecuencias.

Actividad: Mediana     Descripción:

Calcula en tu cuaderno la mediana para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tegas en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividades:

  1. Modifica las frecuencias y observa como puede variar el valor de la mediana.
  2. ¿Cuál es el valor menor que puede tomar? ¿Y el mayor?

video
Mediana
Tutorial (15´23")     Sinopsis:

Mediana correspondiente a una muestra:

  • Definición.
  • Ejemplos.
Ejemplo 1 (datos no agrupados) (4'48")     Sinopsis:

Cálculo de la mediana para datos no agrupados. Ejemplos.

Ejemplo 2 (datos no agrupados) (6'09")     Sinopsis:

Cálculo de la mediana para datos no agrupados. Ejemplos.

Ejemplo 3 (datos agrupados) (14'24")     Sinopsis:

Cálculo de la mediana para datos agrupados sin intervalos. Ejemplos.

Ejemplo 4 (datos en intervalos) (7'59")     Sinopsis:

Cálculo de la mediana para datos agrupados en intervalos. Ejemplos.

Actividades

video
Ejercicios: Parámetros de centralización
Ejercicio 1 (6'50")     Sinopsis:

Cálculo de la moda y la media para datos agrupados con o sin intervalos.

Ejercicio 2 (9'40")     Sinopsis:

Cálculo de la media, mediana y moda para datos no agrupados.

Ejercicio 3 (13'46")     Sinopsis:

Cálculo de la media, mediana y moda para datos agrupados en intervalos.

Ejercicio 4 (14'56")     Sinopsis:

Parámetros de centralización.

Ejercicio 5 (5´02")     Sinopsis:

Media aritmética, mediana y moda correspondiente a una muestra de 30 estudiantes en los que se observó el número de horas que pelan la pava diariamente.

Ejercicio 6 (9´08")     Sinopsis:

Media aritmética, mediana y moda correspondiente a una muestra de 30 estudiantes en los que se observó el número de horas que estudian diariamente.

Parámetros de dispersión

Rango o recorrido

Se define el rango o recorrido como la diferencia entre el mayor y el menor de los valores de la variable. Se representa por R. Nos indica un intervalo en el que están comprendido todos los datos.

Rango o recorrido     Descripción:

Ejemplos con los que podrás aprender a calcular el rango de una distribución estadística.

Autoevaluación: Rango o recorrido     Descripción:

Actividades para comprobar lo que has aprendido sobre el cálculo del rango de una distribución estadística.

Desviación media

  • La diferencia entre cada dato y la media aritmética del grupo se llaman desviaciones respecto a la media.
  • Desviación media de un conjunto de datos es la media aritmética de los valores absolutos de las desviaciones respecto a la media.

Desviaciones respecto a la media     Descripción:

La diferencia entre cada dato y la media aritmética del grupo se llaman desviaciones respecto a la media. Ejemplos.

Desviación media     Descripción:

Desviación media de un conjunto de datos es la media aritmética de los valores absolutos de las desviaciones respecto a la media. Ejemplos.

Autoevaluación: Desviación media     Descripción:

Ejercicios de autoevaluación sobre el cálculo de la desviación media.

Rango y desviación media     Descripción:

Actividades en la que podrás aprender a calcular el rango y la deviación media de una distribución estadística.

Varianza y desviación típica

Se define la varianza como la media aritmética de los cuadrados de las desviaciones respecto de la media. Es decir:

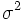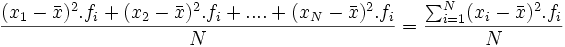
\sigma^2\ = \frac{(x_1 - \bar x)^2.f_i + (x_2 - \bar x)^2.f_i + ....+(x_N - \bar x)^2.f_i} {N}={\sum_{i=1}^N (x_i - \bar x)^2.f_i \over N}

Se calcula más facilmente, con la siguiente fórmula equivalente:

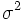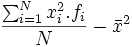
\sigma^2\ = {\sum_{i=1}^N x_i^2.f_i \over N} - \bar x^2
Se define la desviación típica como la raíz cuadrada positiva de la varianza.

Si la variable es continua, el cálculo se hace de la misma forma pero utilizando como xi las marcas de clase: los valores centrales de cada intervalo o la media aritmética de los extremos de cada intervalo.

Varianza y desviación típica     Descripción:

Actividades en la que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística.

Varianza y desviación típica     Descripción:

Ejemplos con los que podrás aprender a calcular la deviación típica y la varianza de una distribución estadística.

Autoevaluación: Varianza y desviación típica     Descripción:

Ejercicios con los que podrás comprobar lo aprendido sobre el cálculo de la deviación típica y la varianza de una distribución estadística.

Actividad 1: ''Varianza y desviación típica (Variable discreta)     Descripción:

Calcula en tu cuaderno la varianza y desviación típica para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tengas en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividades:

  1. Modifica las frecuencias y observa como puede variar el valor de la desviación típica.
  2. ¿Cuál es el menor valor que puede tomar la desviación típica? Intenta construir un caso con desviación típica igual a 0. Justifica la respuesta.
  3. ¿Cuál es el mayor valor que puede tomar la desviación media? Justifica la respuesta.
  4. ¿Cómo hay que modificar las frecuencias para que aumente la desviación típica?¿Y para que disminuya?
Actividad 2: ''Varianza y desviación típica (Variable continua)     Descripción:

Calcula en tu cuaderno el la varianza y desviación típica para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos. Una vez que lo tengas en tu cuaderno, calcúlala con la escena y compara los resultados.

Actividades:

  1. Modifica las frecuencias y observa como puede variar el valor de la desviación típica.
  2. ¿Cuál es el menor valor que puede tomar la desviación típica? Intenta construir un caso con desviación típica igual a 0. Justifica la respuesta.
  3. ¿Cuál es el mayor valor que puede tomar la desviación media? Justifica la respuesta.
  4. ¿Cómo hay que modificar las frecuencias para que aumente la desviación típica?¿Y para que disminuya?

video
Vararianza y desviación típica
Tutorial (caso variable discreta) (5'37")     Sinopsis:

Cálculo de la vararianza y de la desviación típica. Ejemplos.

Tutorial (caso variable continua) (4'51")     Sinopsis:

Cálculo de la vararianza y de la desviación típica. Ejemplos.

Actividades

video
Parámetros de dispersión
Tutorial (9´38")     Sinopsis:

Parámetros de dispersión de una muestra:

  • Recorrido.
  • Varianza.
  • Desviación típica.
Ejercicio 1 (11'34")     Sinopsis:

Determina los parámetros de dispersión de una muestra de 100 estudiantes en los que se observó el número de hermanos.

Ejercicio 2 (14'03")     Sinopsis:

Determina los parámetros de dispersión de una muestra de 50 piezas en las que se observó el peso de cada una.

Ejercicio 3 (14'16")     Sinopsis:

Ejercicio sobre una distribución de notas de 20 alumnos. Deberás elaborar una tabla de frecuencias para calcular la media, la varianza, la desviación típica y la desviación media.

Ejercicio 4 (17'05")     Sinopsis:

Ejercicio sobre una distribución de estaturas de 30 alumnos. Deberás elaborar una tabla de frecuencias para calcular la media, la varianza, la desviación típica y la desviación media.

Interpretación conjunta de la media y la desviación típica

De todas los parámetros estudiados, los más significativos son la media para las medidas de centralización y la desviación típica para las medidas de dispersión.

Vamos a hacer un estudio conjunto de ambas para entender mejor su significado.

La media aritmética es el centro de gravedad de la distribución estadística. Si nos imaginamos el diagrama de barras o el histograma de frecuencias apoyado en un punto del eje horizontal de forma que quedase en equilibrio, el valor de este punto en dicho eje sería el valor de la media.

Como ya hemos comentado, no es suficiente con un parámetro de centralización, es necesario un parámetro de dispersión que nos indique si los datos estudiados están más concentrados o más dispersos. Y este parámetro de dispersión va a ser la desviación típica. Lógicamente si los datos están más concentrados la desviación típica será menor, y si los datos están más dispersos la desviación típica será mayor.

Actividad: Interpretación conjunta de la media y la desviación típica     Descripción:

Representa, en la escena, el diagrama de barras para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.

Actividades:

Modifica los valores de las frecuencias, y si quieres introduce más valores de la variable, hasta que el número de datos sea, por ejemplo, N=100. Construye ejemplos con las siguientes características:

  1. Dale a todas las frecuencias el mismo valor (el que quieras). ¿Cuánto vale la media? ¿Es lógico este resultado? ¿Cuánto vale la desviación típica?
  2. Ve disminuyendo en varios pasos las frecuencias de los valores centrales y aumentando por igual las frecuencias de los valores extremos, sin que varíe la media ni el número de datos. ¿Qué ocurre con la desviación típica? ¿Por qué sucede esto?
  3. Realiza ahora el procedimiento inverso, ve aumentando en varios pasos las frecuencias de los valores centrales y disminuyendo por igual las frecuencias de los valores extremos, sin que varíe la media ni el número de datos. ¿Qué ocurre con la desviación típica? ¿Por qué sucede esto?
  4. ¿Cómo será una variable estadística con desviación típica igual a 0? ¿Compruébalo en la escena?

Coeficiente de variación. Si hemos realizado un estudio estadístico en dos poblaciones diferentes, y queremos comparar resultados, no podemos acudir a la desviación típica para ver la mayor o menor homogeneidad de los datos, sino a otro parámetro nuevo, llamado coeficiente de variación y que se define como el cociente entre la desviación típica y la media.

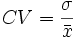
{CV}={\sigma \over \bar x}

ejercicio
Ejemplo:

En una exposición de ganado estudiamos un conjunto de vacas con una media de 500 kilos y una desviación típica de 50 kilos. Y observamos también un conjunto de perros con una media de 40 kilos y una desviación típica de 10 kilos. ¿Qué grupo de animales es más homogéneo?

Solución:

Un razonamiento falso sería decir que el conjunto de perros es más homogéneo porque su desviación típica es más pequeña, pero si calculamos el coeficiente de variación para ambos:

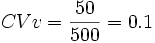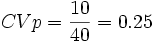
{CVv}={50 \over 500}= 0.1 ; {CVp}={10 \over 40}= 0.25

Por tanto, es más homogéneo el conjunto de las vacas.

Coeficiente de variación     Descripción:

Actividades en la que podrás aprender a calcular el coeficiente de variación de una distribución estadística.

Ejercicios

Ejercicio 1 (22'07")     Sinopsis:

Tutorial que explica, por medio de un sencillo ejercicio, los parámetros de dispersión: rango, desviación media, desviación típica o estándar y el coeficiente de variación.

Ejercicio 2 (19'09")     Sinopsis:

Tutorial que explica los parámetros de centralización (moda, mediana, media) y de dispersión (rango, desviación media, desviación típica, coeficiente de variación), mediante un sencillo ejercicio de los personajes de los Simpson. En este ejercicio aparecen pocos en la muestra por lo que se utiliza la definición de cada uno de los parámetros para su cálculo sin necesidad de recurrir a una tabla de frecuencias ni a complejas fórmulas.

Ejercicio 3 (13'53")     Sinopsis:

Ejercicio de cálculo de los parámetros de centralización y dispersión.

Obtenido de "http://maralboran.org/wikipedia/index.php/Plantilla:Par%C3%A1metros_estad%C3%ADsticos"
Herramientas personales
* AVISO: Para que te funcionen los applets de Java debes usar Internet Explorer y seguir las instrucciones de la Ayuda del menu de la izquierda