Plantilla:Cálculo del m.c.m.
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 11:17 8 ago 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 11:19 8 ago 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| - | + | {{Teorema_sin_demo|titulo=Procedimiento | |
| - | {{Teorema_sin_demo|titulo=Cálculo del mínimo común múltiplo | + | |enunciado=Para obtener el m.c.m. de dos o más números, se descomponen los números en factores primos y se toman todos los factores elevados al mayor exponente.}} |
| - | |enunciado=:Para obtener el m.c.m. de dos o más números, se descomponen los números en factores primos y se toman todos los factores elevados al mayor exponente.}} | + | |
| {{p}} | {{p}} | ||
| {{Ejemplo_simple | {{Ejemplo_simple | ||
Revisión de 11:19 8 ago 2017
Procedimiento
Para obtener el m.c.m. de dos o más números, se descomponen los números en factores primos y se toman todos los factores elevados al mayor exponente.
- Calcula el m.c.m.(24,60):
- Primer método:
- Múltiplos de 24: 24, 48, 72, 96, 120, 144,...
- Múltiplos de 60: 60, 120, 180, ...
- m.c.m.(24,60)= 120
- Segundo método:
- Descomponemos 24 y 60 en sus factores primos:
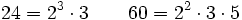
- Multiplicando todos los factores elevados al mayor exponente:
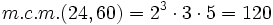
Tutorial que explica el significado del mínimo común múltiplo, es decir "¿qué es?" y las distintas técnicas para su cálculo, desde mentalmente o bien obteniendo los múltiplos de los números, para el caso de número pequeños, o el algoritmo general.
- 00:00 a 06:33: ¿Qué es el Mínimo Común Múltiplo? Método de extracción de múltiplos.
- 06:33 a 11:18: Método general para calcular el MCM. Ejemplos.
Cálcula el mínimo común múltiplo de:
a) 12 y 18
b) 360 y 84
c) 40, 72 y 300
Cálcula el mínimo común múltiplo de:
a) 4 y 3
b) 4 y 30
c) 75, 25 y 15
d) 98, 10 y 45
Cálcula el mínimo común múltiplo de:
a) 6 y 8
b) 14, 21 y 28
Cálcula el mínimo común múltiplo de:
a) 4 y 6
b) 9, 10 y 15

