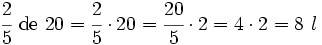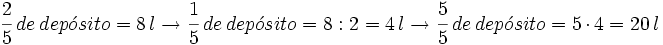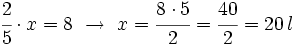Problemas con fracciones (2º ESO)
De Wikipedia
| Revisión de 17:40 31 ago 2017 Coordinador (Discusión | contribuciones) (→Cálculo de la fracción de una cantidad) ← Ir a diferencia anterior |
Revisión de 09:14 1 sep 2017 Coordinador (Discusión | contribuciones) (→Problemas) Ir a siguiente diferencia → |
||
| Línea 53: | Línea 53: | ||
| |descripcion=Ejercicios de autoevaluación sobre fracciones. | |descripcion=Ejercicios de autoevaluación sobre fracciones. | ||
| |url1=http://www.vitutor.com/di/r/b_1e1.html | |url1=http://www.vitutor.com/di/r/b_1e1.html | ||
| + | }} | ||
| + | |||
| + | ==Problemas con sumas y restas de fracciones== | ||
| + | {{Ejemplo|titulo=Ejemplo 1: ''Cálculo de la parte conocido el total'' | ||
| + | |enunciado=Tras un fabuloso día de pesca Juan decide compartir 3 kilos de pescado con sus dos hermanos, Antonio y Jaime. A Jaime le regala dos quintos y a Antonio un tercio. | ||
| + | |||
| + | a) ¿Qué fracción le queda a Juan? | ||
| + | b)¿Cuántos kilos de pescado le queda a Juan? | ||
| + | |sol= | ||
| + | a) Como las fracciones correspondientes a Jaime y Antonio se refieren al total de la pesca, primero tendremos que sumarlas para ver que fracción regala Juan: | ||
| + | |||
| + | <center><math>\cfrac{2}{5}+\cfrac{1}{3}=\cfrac{6}{15}+\cfrac{5}{15}=\cfrac{11}{15}</math></center> | ||
| + | |||
| + | En consecuencia, a Juan le corresponderá: | ||
| + | |||
| + | <center><math>1-\cfrac{11}{15}=\cfrac{15-11}{15}=\cfrac{4}{15}</math></center> | ||
| + | |||
| + | b) Para el segundo apartado recurriremos a lo aprendido en el apartado anterior sobre cómo funciona la fracción como operador, ya que tendremos que calcular los 4/15 de 3 kilos: | ||
| + | |||
| + | <center><math>\cfrac{4}{15} \cdot 3=\cfrac{4 \cdot 3}{15}=\cfrac{12}{15}=0.8 ~kg = 800~g</math></center> | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Ejemplo|titulo=Ejemplo 1: ''Cálculo del total conocida la parte'' | ||
| + | |enunciado=Tras un fabuloso día de pesca Juan decide compartir la pesca con sus dos hermanos, Antonio y Jaime. A Jaime le regala dos quintos, a Antonio un tercio y él se queda con 800 g. ¿Cuánto kilos pescó Juan? | ||
| + | |sol= | ||
| + | Al igual que en el ejemplo anterior, como las fracciones correspondientes a Jaime y Antonio se refieren al total de la pesca, primero tendremos que sumarlas para ver que fracción regala Juan: | ||
| + | |||
| + | <center><math>\cfrac{2}{5}+\cfrac{1}{3}=\cfrac{6}{15}+\cfrac{5}{15}=\cfrac{11}{15}</math></center> | ||
| + | |||
| + | En consecuencia, a Juan le corresponderá: | ||
| + | |||
| + | <center><math>1-\cfrac{11}{15}=\cfrac{15-11}{15}=\cfrac{4}{15}</math></center> | ||
| + | |||
| + | A continuación, para averiguar el total de la pesca, plantearemos la siguiente ecuación, igual que hacíamos en el apartado anterior sobre el uso de la fracción como operador: | ||
| + | |||
| + | Sea <math>x\;</math> el total de kilos que pescó Juan: | ||
| + | |||
| + | <center><math>\cfrac{4}{15} \cdot x=0.8 \rightarrow x=\cfrac{15 \cdot 0.8}{4}=3~kg</math></center> | ||
| }} | }} | ||
Revisión de 09:14 1 sep 2017
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. )
Veamos distintos casos de problemas con fracciones que nos podemos encontrar.
Cálculo de la fracción a partir del total y la parte
En este tipo de problemas nos dan dos cantidades: una que representa el total y otra que representa la parte, y se nos pide averiguar la fracción que representa la parte con respecto al total.
Procedimiento
Para calcular la fracción a partir del total y la parte, se divide la parte entre el total y se simplifica la fracción resultante.
Ejemplo: Cálculo de la fracción de una cantidad
En una empresa hay 1200 trabajadores, de los que 420 son hombres. ¿Qué fracción de mujeres y qué fracción de hombres trabajan en esta empresa?
La fracción de hombres será:
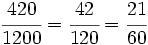
En consecuencia, la de mujeres será:
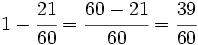
La fracción como operador
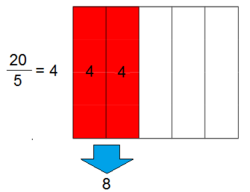
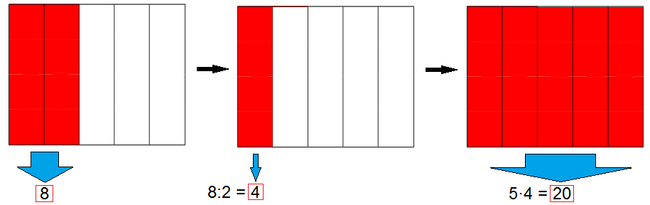
Supongamos que tenemos una cierta cantidad (que llamaremos "el total") y que queremos saber cuánto es una determinada fracción de dicha cantidad (que llamaremos "la parte"). En tal caso, diremos que la fracción actúa como operador de dicha cantidad y procederemos de la siguiente manera : Dividimos la cantidad total entre el denominador, para calcular cuantos grupos del tamaño del denominador podemos hacer, y multiplicamos por el numerador, que representa la cantidad de esos grupos que tomamos.
Fracción de una cantidad
Para calcular una fracción a/b de una cantidad C se divide la cantidad entre el denominador y se multiplica por el numerador. (También podemos multiplicar primero por el numerador y dividir después por denominador, o incluso calcular el valor de la fracción y multiplicarlo por C).
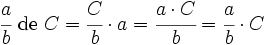
Ejemplo 1: Cálculo de la parte conocido el total
Si de un depósito de agua, en el que caben 20 l, sólo están llenas las 2/5 partes, ¿cuánta agua hay en el depósito?
Actividad para practicar el cálculo de la fracción de una cantidad de forma guiada.
Ejemplo 2: Cálculo del total conocida la parte
Un depósito de agua tiene 8 l, que son las 2/5 partes de su capacidad. ¿Cuál es la capacidad total del depósito?
La fracción como operador. Ejemplos.
Tutorial en el que se dan los conceptos matemáticos de proporción y se explica/justifica como calcular proporciones de cantidades o bien la cantidad a la que se le aplicó una proporción.
Cómo se calcula la fracción de un número.
He pagado 2/5 partes de una bici que costaba 90€. ¿Cuánto me falta por pagar?
He pagado 2/5 partes de una bici y me faltan 90€ por pagar. ¿Cuánto costaba la bici?
He pagado 2/5 partes de una bici que suponen 90€ del total. ¿Cuánto costaba la bici?
Problemas sencillos con fracciones resueltos.
Ejercicios de autoevaluación sobre fracciones.
Problemas con sumas y restas de fracciones
Ejemplo 1: Cálculo de la parte conocido el total
Tras un fabuloso día de pesca Juan decide compartir 3 kilos de pescado con sus dos hermanos, Antonio y Jaime. A Jaime le regala dos quintos y a Antonio un tercio.
a) ¿Qué fracción le queda a Juan? b)¿Cuántos kilos de pescado le queda a Juan?
a) Como las fracciones correspondientes a Jaime y Antonio se refieren al total de la pesca, primero tendremos que sumarlas para ver que fracción regala Juan:
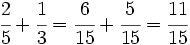
En consecuencia, a Juan le corresponderá:
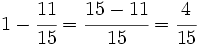
b) Para el segundo apartado recurriremos a lo aprendido en el apartado anterior sobre cómo funciona la fracción como operador, ya que tendremos que calcular los 4/15 de 3 kilos:
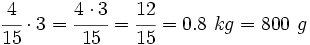
Ejemplo 1: Cálculo del total conocida la parte
Tras un fabuloso día de pesca Juan decide compartir la pesca con sus dos hermanos, Antonio y Jaime. A Jaime le regala dos quintos, a Antonio un tercio y él se queda con 800 g. ¿Cuánto kilos pescó Juan?
Al igual que en el ejemplo anterior, como las fracciones correspondientes a Jaime y Antonio se refieren al total de la pesca, primero tendremos que sumarlas para ver que fracción regala Juan:
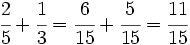
En consecuencia, a Juan le corresponderá:
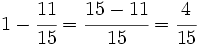
A continuación, para averiguar el total de la pesca, plantearemos la siguiente ecuación, igual que hacíamos en el apartado anterior sobre el uso de la fracción como operador:
Sea  el total de kilos que pescó Juan:
el total de kilos que pescó Juan:
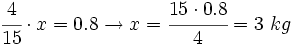
Problemas
Problemas con fracciones.
Problemas con fracciones.
4 problemas:
- Una caja contiene 60 galletas. Raúl se come 1/3 y Manuel 2/5. ¿Cuántas galletas se ha comido cada uno?
- Pedro ha recorrido en bici 6 km, que son 3/4 de la etapa de hoy. ¿Cuál es el recorrido total de la etapa?
- Alicia tiene 30€ de paga mensual. La primera semana gastó 2/5. La segunda gastó 5/6 de lo que le quedaba. ¿Cuánto gastó cada semana?.¿Cuánto le queda?
- Tenemos que vaciar una piscina. Sacamos por la mañana 2/5 del agua y por la tarde 1/4 de lo que quedaba. Si la final del día había 180 litros, ¿cuál es la capacidad de la piscina?.
2 problemas:
- Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 del total. ¿Cuánto trasladará el tercero?
- Tres camiones tienen que trasladar 2400 kg de escombros. El primer camión se lleva 1/3 y después, el segundo, 2/5 de lo que queda. ¿Cuánto trasladará el tercero?
Problemas con fracciones.
Problemas con fracciones.
Problemas con fracciones.
Mi padre se ha comido 1/8 de la tableta de turrón y mi madre 2/7 de lo que quedaba. Si costó 4€, ¿cuántos céntimos se comió cada uno?.¿Qué fracción queda?
Problemas resueltos sobre fracciones.