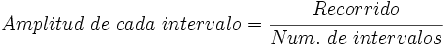Análisis descriptivo
De Wikipedia
| Revisión de 17:45 24 jun 2007 Juanmf (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 17:48 24 jun 2007 Juanmf (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| + | =Tablas= | ||
| ==Tablas estadísticas== | ==Tablas estadísticas== | ||
| Son utilizadas para organizar los datos. Según el número de observaciones y según el recorrido de la variable estadística, tenemos los siguientes tipos de tablas estadísticas: | Son utilizadas para organizar los datos. Según el número de observaciones y según el recorrido de la variable estadística, tenemos los siguientes tipos de tablas estadísticas: | ||
| Línea 164: | Línea 165: | ||
| ::d) ¿Cómo se puede obtener el porcentaje de individuos que presentan cada uno de los valores de la variable? | ::d) ¿Cómo se puede obtener el porcentaje de individuos que presentan cada uno de los valores de la variable? | ||
| }} | }} | ||
| + | {{p}} | ||
| + | =Gráficos= | ||
| Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar: | Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar: | ||
| ==Diagrama de barras== | ==Diagrama de barras== | ||
Revisión de 17:48 24 jun 2007
Tabla de contenidos |
Tablas
Tablas estadísticas
Son utilizadas para organizar los datos. Según el número de observaciones y según el recorrido de la variable estadística, tenemos los siguientes tipos de tablas estadísticas:
Tablas Tipo I
Cuando el tamaño de la muestra y el recorrido (mayor valor menos el valor menor) de la variable son pequeños, por ejemplo si tenemos una muestra de las edades de 5 personas, por lo que no hay que hacer nada especial simplemente anotarlas de manera ordenada en filas o columnas.
Edad de los 5 miembros de una familia:
5, 8, 16, 38, 45
Tablas Tipo II
Cuando el tamaño de la muestra es grande y el recorrido de la variable es pequeño, por lo que hay valores de la variable que se repiten.
Por ejemplo, si preguntamos el número de personas activas que hay en 50 familias obtenemos la siguiente tabla:
Personas Activas en 50 familias
| 2 | 1 | 2 | 2 | 1 | 2 | 4 | 2 | 1 | 1 |
| 2 | 3 | 2 | 1 | 1 | 1 | 3 | 4 | 2 | 2 |
| 2 | 2 | 1 | 2 | 1 | 1 | 1 | 3 | 2 | 2 |
| 3 | 2 | 3 | 1 | 2 | 4 | 2 | 1 | 4 | 1 |
| 1 | 3 | 4 | 3 | 2 | 2 | 2 | 1 | 3 | 3 |
Podemos observar que la variable toma valores comprendidos entre 1 y 4, por lo que precisaremos una tabla en la que resumamos estos datos quedando la siguiente tabla:
| Personas activas | Número de familias |
| 1 | 16 |
| 2 | 20 |
| 3 | 9 |
| 4 | 5 |
| total | 50 |
Tablas Tipo III
Cuando el tamaño de la muestra y el recorrido de la variable son grandes, por lo que será necesario agrupar en intervalos los valores de la variable. Tambien obligatorio usarla cuando la variable sea cuantitativa continua.
Por ejemplo si a un grupo de 30 alumnos les preguntamos el dinero que en ese momento tienen ahorrado, nos encontramos con los siguientes datos:
| 450 | 1152 | 250 | 300 | 175 | 80 | 25 | 2680 | 605 | 785 |
| 1595 | 2300 | 5000 | 1200 | 100 | 5 | 180 | 200 | 675 | 500 |
| 375 | 1500 | 205 | 985 | 185 | 125 | 315 | 425 | 560 | 1100 |
La variable estadística tiene un recorrido muy grande, (Mayor valor - Menor valor = 5000 - 5 = 4995), por lo que sí queremos hacer una tabla con estos datos tendremos que tomar intervalos. Para decidir la amplitud de los intervalos, necesitaremos decidir ¿cuántos intervalos queremos?. Normalmente se suele trabajar con no más de 10 o 12 intervalos.
|
|
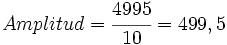
Por lo que tomaremos intervalos de amplitud 500
Debemos tener en cuenta las siguientes consideraciones:
Tomar pocos intervalos implica que la "pérdida de información" sea mayor.
Los intervalos serán siempre Cerrados por la izquierda y Abiertos por la Derecha [Li-1 , Li).
Con estas recomendaciones tendremos la siguiente tabla:
| Intervalo | Nº alumnos |
| [0,500) | 16 |
| [500,1000) | 6 |
| [1000,1500) | 3 |
| [1500,2000) | 2 |
| [2000,2500) | 1 |
| [2500,3000) | 1 |
| [3000,3500) | 0 |
| [3500,4000) | 0 |
| [4000,4500) | 0 |
| [4500,5000) | 0 |
| [5000,5500) | 1 |
Tablas de frecuencias
Ahora iremos añadiendo más columnas según los cálculos y la información que necesitemos. Podemos ir completando la tabla con las frecuencias, que definimos a continuación:
- Frecuencia absoluta. Es el número de veces que aparece cualquier valor de la variable. Se representa por fi. En algunos libros de texto nos la encontraremos representada por ni.
- Frecuencia absoluta acumulada. Es la suma de la frecuencia absoluta de un valor de la variable con todos los anteriores. Se representa por Fi.
- Frecuencia relativa. Es el cociente entre la frecuencia absoluta y el número de datos (N). Se representa por hi. En algunos libros de texto nos la encontraremos representada por ri. Al multiplicarla por 100 obtenemos el porcentaje de individuos que presentan esta característica.
- Frecuencia relativa acumulada. Es la suma de la frecuencia relativa de un valor de la variable con todos los anteriores. También se puede definir como el cociente entre la frecuencia absoluta acumulada y el número total de datos. Se representa por Hi.
En las siguientes escenas puedes construir la tabla de frecuencias para variables discretas y continuas.
Actividades
|
Actividad Interactiva: Tablas de frecuencias
1. Variable cuantitativa discreta.
Actividad: Construye en tu cuaderno la tabla para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, constrúyela con la escena y compara los resultados.
2. Variable cuantitativa continua.
Actividad: Construye en tu cuaderno la tabla para el ejemplo de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66. Necesitas agrupar los datos en intervalos. Una vez que la tienes en tu cuaderno, constrúyela con la escena y compara los resultados. |
Como puedes observar no se han tenido en cuenta las variables cualitativas. Esto se debe a que al no trabajar con números no se pueden hacer operaciones. Únicamente tendría sentido en la tabla construir las columnas de frecuencias absolutas y relativas, pero no las acumuladas. En el siguiente apartado de gráficos estadísticos también se podrían representar, pero para los apartados de cálculo de parámetros no podremos trabajar con ellas. si tienes interés en alguna representación, sustituye los valores la variable por los números que quieras y represéntalas o construye la tabla
|
Actividades
|
Gráficos
Una vez construida la tabla de frecuencias, vamos a representar mediante distintos gráficos el estudio realizado. Entre los gráficos más utilizado podemos destacar:
Diagrama de barras
Consiste en dos ejes perpendiculares y una barra o rectángulo para cada valor de la variable. Normalmente, se suele colocar en el eje horizontal los valores de la variable (aunque también se puede hacer en el vertical). El otro eje se gradúa según los valores de las frecuencias. La representación gráfica consiste en dibujar una barra o un rectángulo para cada uno de los valores de la variable de altura igual a su frecuencia.
Histograma
Es un caso particular del diagrama anterior en el caso de variables continuas. Si los intervalos son correlativos, los rectángulos aparecen pegados en la representación gráfica. En caso de que la amplitud de los intervalos no se igual para todos, hay que hacer coincidir el área del rectángulo con la frecuencia del intervalo. Un ejemplo muy utilizado de histograma es una pirámide de población.
Polígono de frecuencias
Representamos dos ejes perpendiculares y representamos en el horizontal los valores de la variable y en el vertical las frecuencias. Representamos los puntos que tiene por primera coordenada el valor de la variable y por segunda el valor de la frecuencia. Uniendo todos los puntos obtenemos una línea poligonal que es la representación que buscamos.
Diagrama de sectores
Consiste en dividir un círculo en tantos sectores como valores de la variable. La amplitud de cada sector debe ser proporcional a la frecuencia del valor correspondiente.
Actividades
|
Actividades Interactivas: Gráficos estadísticos
Actividad 1. Diagrama de barras.
Actividad: Representa en tu cuaderno el diagrama de barras para el ejemplo número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2. Una vez que la tienes en tu cuaderno, represéntala con la escena y compara los resultados.
Actividad 2. Histograma.
Actividad: Representa en tu cuaderno el histograma para el ejemplo del número de la estatura: 1.59, 1.75, 1.71, 1.85, 1.64, 1.62, 1.66, 1.60, 1.63, 1.76, 1.66, según hayas agrupados los datos en intervalos.Una vez que lo tienes en tu cuaderno, represéntalo con la escena y compara los resultados.
Actividad 3. Polígono de frecuencias.
Actividad: Representa en tu cuaderno el polígono de frecuencias para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que lo tienes en tu cuaderno, represéntalo con la escena y compara los resultados.
Actividad 4. Diagrama de sectores.
Actividad: Representa en tu cuaderno el polígono de frecuencias para el ejemplo del número de hermanos: 2, 3, 2, 3, 3, 3, 3, 4, 2, 2, 2.Una vez que lo tienes en tu cuaderno, represéntalo con la escena y compara los resultados. |
|
Actividad Actividad 1:
|