Plantilla:Poliedros: pirámide
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 10:07 26 sep 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 10:08 26 sep 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 9: | Línea 9: | ||
| |sinopsis=Pirámide: definición y elementos. | |sinopsis=Pirámide: definición y elementos. | ||
| |url1=https://www.youtube.com/watch?v=ZyftAKtrAHc&index=19&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm | |url1=https://www.youtube.com/watch?v=ZyftAKtrAHc&index=19&list=PLVEkI8DcwbMvQ6jn4xXCRHpLeLVkeWDkm | ||
| + | }} | ||
| + | {{p}} | ||
| + | {{Geogebra_enlace | ||
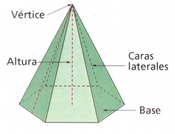
| + | |descripcion=En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados. | ||
| + | |enlace=[https://ggbm.at/XrcfnFaT Elementos de una pirámide] | ||
| }} | }} | ||
| {{p}} | {{p}} | ||
| Se pueden clasificar: | Se pueden clasificar: | ||
| - | + | {{p}} | |
| {{Caja_Amarilla|texto= | {{Caja_Amarilla|texto= | ||
| *'''Atendiendo a sus bases:''' En función del polígono base, las pirámides pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.{{p}} | *'''Atendiendo a sus bases:''' En función del polígono base, las pirámides pueden ser de base triangular, cuadrangular, pentagonal, hexagonal, etc.{{p}} | ||
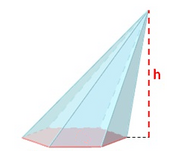
| *'''Atendiendo a su inclinación:''' Si la proyección ortogonal del vértice sobre la base coincide con su centro, la pirámide es '''recta''', si no , es '''oblicua'''. | *'''Atendiendo a su inclinación:''' Si la proyección ortogonal del vértice sobre la base coincide con su centro, la pirámide es '''recta''', si no , es '''oblicua'''. | ||
| *'''Atendiendo a su regularidad:''' Una pirámide es '''regular''' si su base es un polígono regular. En caso contrario es '''irregular'''. En una pirámide regular, todas las aristas laterales son iguales y las caras laterales son triángulos isósceles iguales. La altura de cada uno de ellos se llama '''apotema de la pirámide'''.}} | *'''Atendiendo a su regularidad:''' Una pirámide es '''regular''' si su base es un polígono regular. En caso contrario es '''irregular'''. En una pirámide regular, todas las aristas laterales son iguales y las caras laterales son triángulos isósceles iguales. La altura de cada uno de ellos se llama '''apotema de la pirámide'''.}} | ||
| - | {{p}} | + | |
| - | {{Geogebra_enlace | + | |
| - | |descripcion=En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados. | + | |
| - | |enlace=[https://ggbm.at/XrcfnFaT Elementos de una pirámide] | + | |
| - | }} | + | |
| {{p}} | {{p}} | ||
| {{Video_enlace_estudiia | {{Video_enlace_estudiia | ||
Revisión de 10:08 26 sep 2017
Pirámide: definición y elementos. En esta escena podrás ver el vértice, las apotemas y la altura de una pirámide regular con polígono básico de hasta 8 lados. Se pueden clasificar:
Clasificación de las pirámides. Definiciones, elementos y propiedades. |