Troncos de pirámides (2º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 19:32 26 sep 2017 Coordinador (Discusión | contribuciones) (→Tronco de pirámide regular) ← Ir a diferencia anterior |
Revisión de 19:33 26 sep 2017 Coordinador (Discusión | contribuciones) (→Desarrollo plano del tronco de pirámide) Ir a siguiente diferencia → |
||
| Línea 36: | Línea 36: | ||
| {{Caja_Amarilla|texto=Si representamos en un plano todas las caras de un tronco de pirámide, de forma contigua, obtenemos lo que se denomina '''desarrollo plano''' del tronco de pirámide.}} | {{Caja_Amarilla|texto=Si representamos en un plano todas las caras de un tronco de pirámide, de forma contigua, obtenemos lo que se denomina '''desarrollo plano''' del tronco de pirámide.}} | ||
| {{p}} | {{p}} | ||
| - | Fíjate en el siguiente tronco de pirámide cuadrangular. Si la cortásemos adecuadamente siguiendo ciertas aristas, podríamos desplegarlo como se muestra en la siguiente figura. | + | Fíjate en el siguiente tronco de pirámide cuadrangular. Si la cortásemos adecuadamente, siguiendo ciertas aristas, podríamos desplegarlo como se muestra en la siguiente figura. |
| {{p}} | {{p}} | ||
| [[Imagen:deasarrollo_tronco_piramide.gif|center|500px]]<br><center>Desarrollo plano de un tronco de pirámide cuadrangular regular<br><sup>''de http://calculo.cc''</sup></center> | [[Imagen:deasarrollo_tronco_piramide.gif|center|500px]]<br><center>Desarrollo plano de un tronco de pirámide cuadrangular regular<br><sup>''de http://calculo.cc''</sup></center> | ||
Revisión de 19:33 26 sep 2017
Menú:
| Enlaces internos | Para repasar | Para ampliar | Enlaces externos |
| Indice Descartes Manual Casio | WIRIS Calculadora |
Tabla de contenidos |
(Pág. 220)
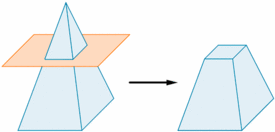
Tronco de pirámide
|  Tronco de pirámide
de http://calculo.cc |
Tronco de pirámide regular
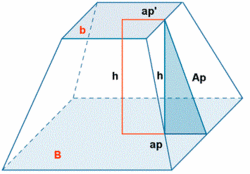
En la figura de la derecha están representados los distintos elementos de un tronco de pirámide regular:
|  Elementos de un tronco de pirámide
de http://calculo.cc |
Desarrollo plano del tronco de pirámide
Si representamos en un plano todas las caras de un tronco de pirámide, de forma contigua, obtenemos lo que se denomina desarrollo plano del tronco de pirámide.
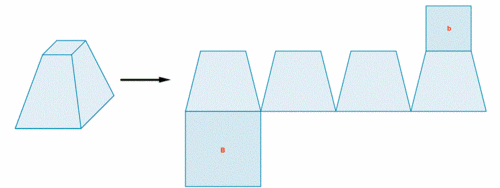
Fíjate en el siguiente tronco de pirámide cuadrangular. Si la cortásemos adecuadamente, siguiendo ciertas aristas, podríamos desplegarlo como se muestra en la siguiente figura.
Desarrollo plano de un tronco de pirámide cuadrangular regular
de http://calculo.cc
de http://calculo.cc
Superficie del tronco de pirámide
La superficie o área del tronco de pirámide es igual a la suma del área de las dosbase y del área lateral.
- El área de las bases es la suma de las áreas de dos polígonos.
- El área lateral es la suma de las áreas de los trapecios que forman las caras laterales.
 |
|
|
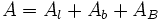
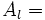Suma áreas trapecios
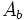: Área de la base superior.
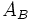: Área de la base inferior.
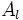: Área lateral.
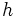: altura.
Ejercicios propuestos
 Ejercicios propuestos: Tronco de pirámide (Pág. 220)
|
