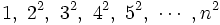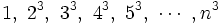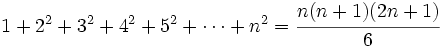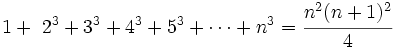Plantilla:Sucesiones potencias
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 07:46 4 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto=Una sucesión de potencias es una sucesión de la forma | {{Caja_Amarilla|texto=Una sucesión de potencias es una sucesión de la forma | ||
| - | <center><math>1, \ 2^m, \ 3^m, \ 4^m, \ 5^m, \ \cdots \ n^m \ \cdots \qquad (m \in \mathbb{N})\;</math></center> | + | <center><math>1, \ 2^m, \ 3^m, \ 4^m, \ 5^m, \ \cdots \ , n^m \ \cdots \qquad (m \in \mathbb{N})\;</math></center> |
| De ellas, las más frecuentes son para los casos m=2 y m=3, que son las sucesiones de '''cuadrados''' y de '''cubos''', respectivamente: | De ellas, las más frecuentes son para los casos m=2 y m=3, que son las sucesiones de '''cuadrados''' y de '''cubos''', respectivamente: | ||
| - | <center><math>1, \ 2^2, \ 3^2, \ 4^2, \ 5^2, \ \cdots \ n^2 \;</math></center> | + | <center><math>1, \ 2^2, \ 3^2, \ 4^2, \ 5^2, \ \cdots \ , n^2 \;</math></center> |
| - | <center><math>1, \ 2^3, \ 3^3, \ 4^3, \ 5^3, \ \cdots \ n^3 \;</math></center> | + | <center><math>1, \ 2^3, \ 3^3, \ 4^3, \ 5^3, \ \cdots \ , n^3 \;</math></center> |
| }} | }} | ||
| {{p}} | {{p}} | ||
Revisión actual
Una sucesión de potencias es una sucesión de la forma

De ellas, las más frecuentes son para los casos m=2 y m=3, que son las sucesiones de cuadrados y de cubos, respectivamente: