Conos (2º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 09:58 7 oct 2017 Coordinador (Discusión | contribuciones) (→Superficie del cono) ← Ir a diferencia anterior |
Revisión actual Coordinador (Discusión | contribuciones) (→Superficie del cono) |
||
| Línea 60: | Línea 60: | ||
| |url1=https://www.youtube.com/watch?v=e3eFmCe4H9o | |url1=https://www.youtube.com/watch?v=e3eFmCe4H9o | ||
| }} | }} | ||
| - | ---- | ||
| {{Video_enlace_math2me | {{Video_enlace_math2me | ||
| - | |titulo1=Tutorial 1 | + | |titulo1=Tutorial 3 |
| |duracion=9'38" | |duracion=9'38" | ||
| |sinopsis=Demostración del área del cono. | |sinopsis=Demostración del área del cono. | ||
| Línea 68: | Línea 67: | ||
| }} | }} | ||
| {{Video_enlace | {{Video_enlace | ||
| - | |titulo1=Tutorial 2 | + | |titulo1=Tutorial 4 |
| |duracion=5'05" | |duracion=5'05" | ||
| |sinopsis=Área del cono. Ejemplo. | |sinopsis=Área del cono. Ejemplo. | ||
Revisión actual
Tabla de contenidos[esconder] |
(Pág. 227)
[editar]
Cono
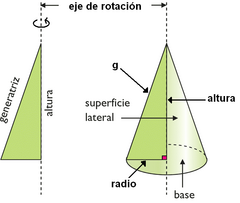
Un cono es un cuerpo de revolución que se obtiene haciendo girar un triángulo rectángulo alrededor de uno de sus catetos. Elementos del cono:
|  |
[editar]
Desarrollo plano del cono
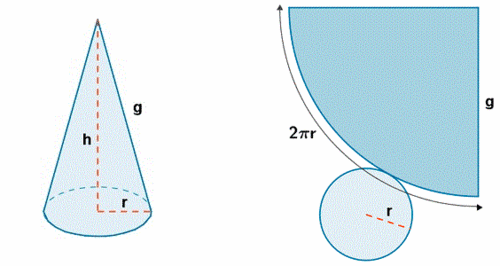
Si representamos en un plano los distintos elementos de la superficie de un cono, de forma contigua, obtenemos lo que se denomina desarrollo plano del cono.
Si cortásemos adecuadamente un cono, podríamos desplegarlos como se muestra en la siguiente imagen.
Desarrollo plano del cono
de http://calculo.cc
de http://calculo.cc
[editar]
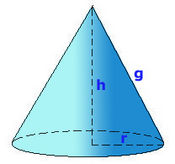
Superficie del cono
La superficie o área del cono es igual a la suma del área de la base y del área lateral.
- El área de la base es el área de un círculo.
- El área lateral es el área de un sector circular.
 |
|
|
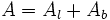
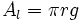
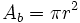
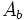: Área de la base.
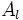: Área lateral.
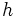: altura.
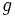: generatriz.
: radio.
[editar]
Ejercicios propuestos
 Ejercicios propuestos: Conos (Pág. 227)
|
