Plantilla:Sucesión de Fibonacci
De Wikipedia
| Revisión de 15:58 10 oct 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 16:01 10 oct 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 44: | Línea 44: | ||
| {{Video_enlace | {{Video_enlace | ||
| |titulo1=La famosa sucesión de Fibonacci | |titulo1=La famosa sucesión de Fibonacci | ||
| - | |sinopsis=Se describe como se genera la sucesión de fibonacci a partir del modelo que usó el matemático italiano Leonardo de Pisa para describir el comportamiento de la cría de conejos | + | |sinopsis=Se describe como se genera la sucesión de Fibonacci a partir del modelo que usó el matemático italiano Leonardo de Pisa para describir el comportamiento de la cría de conejos. |
| - | Para cualquier mes n, el número de conejos Fn estará dado por la relación de recurrencia Fn=Fn-1+Fn-2 con F0=0 y F1=1 | + | |
| + | Para cualquier mes ''n'', el número de conejos ''F<sub>n</sub>'' estará dado por la relación de recurrencia ''F<sub>n</sub>=F<sub>n-1</sub>+F<sub>n-2</sub>'' con ''F<sub>0</sub>=0'' y ''F<sub>1</sub>=1''. | ||
| + | Sus primeros términos son entonces: 0,1,1,2,3,5,8,13,21,34,55,89..... Para generar un nuevo término basta con sumar los dos que le anteceden. | ||
| + | |||
| En el video se muestra adicionalmente que esta es una sucesión monotona creciente no acotada y divergente. | En el video se muestra adicionalmente que esta es una sucesión monotona creciente no acotada y divergente. | ||
| - | Sus primeros términos son entonces: 0,1,1,2,3,5,8,13,21,34,55,89..... | ||
| - | Para generar un nuevo término basta con sumar los dos que le anteceden | ||
| |duracion=11'22" | |duracion=11'22" | ||
| |url1=https://www.youtube.com/watch?v=IppMGZwmLTE | |url1=https://www.youtube.com/watch?v=IppMGZwmLTE | ||
| }} | }} | ||
Revisión de 16:01 10 oct 2017
Ejemplo: La sucesión de Fibonacci y el número áureo
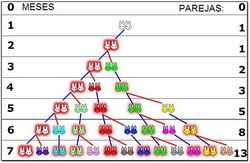
El siguiente problema fue propuesto por Fibonacci, matemático italiano del siglo XIII:
- "Cuántas parejas de conejos se producirán en un año, comenzando con una pareja única, si cada mes cualquier pareja engendra otra pareja, que se reproduce a su vez desde el segundo més?"
a) Escribe la sucesión cuyos términos son lás parejas de conejos que hay cada més. Esta recibe el nombre de sucesión de Fibonacci.
b) Ahora vas a construir la sucesión que se obtiene al dividir cada término entre el anterior. Esa sucesión verás que se aproxima al número áureo (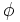 ):
):
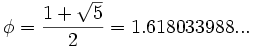
a) Sucesión de Fibonacci:
- Valor inicial: 1 pareja
- Mes 1: 1 pareja (hasta el segundo mes no se reproduce la primera)
- Mes 2: 2 parejas (primera vez que se reproduce)
- Mes 3: 3 parejas (la primera pareja vuelve a reproducirse pero la segunda no lo hace hasta el próximo mes)
- Mes 4: 5 parejas (la primera y la segunda pareja ya se reproducen, la tercera aún no)
- Mes 5: 8 parejas (se reproducen las 3 primeras parejas, las otras dos no)
- Mes 6: 13 parejas (se reproducen las 5 parejas de hace 2 meses, pero las 3 nuevas del mes anterior aún no)
Así se obtiene una sucesión en la que cada término se obtiene a partir de la suma de los dos anteriores:
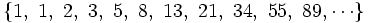
b) Sucesión del número áureo:
Dividiendo cada término entre el anterior, tenemos la sucesión:
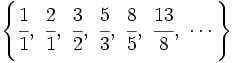
que expresada con decimales vemos que se aproxima al número áureo:
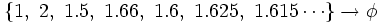
Nota: Leonardo de Pisa (Fibonacci), en su Libro de los ábacos (Liber abacci, 1202, 1228), usa la sucesión que lleva su nombre para calcular el número de pares de conejos n meses después de que una primera pareja comienza a reproducirse (suponiendo que los conejos están aislados por muros, se empiezan a reproducir cuando tienen dos meses de edad, tardan un mes desde la fecundación hasta la parición y cada camada es de dos conejos). Este es un problema matemático puramente independiente de que sean conejos los involucrados. En realidad, el conejo común europeo tiene camadas de 4 a 12 individuos y varias veces al año, aunque no cada mes, pese a que la preñez dura 32 días. El problema se halla en las páginas 123 y 124 del manuscrito de 1228, que fue el que llegó hasta nosotros, y parece que el planteamiento recurrió a conejos como pudiera haber sido a otros seres; es un soporte para hacer comprensible una incógnita, un acertijo matemático.
Se describe como se genera la sucesión de Fibonacci a partir del modelo que usó el matemático italiano Leonardo de Pisa para describir el comportamiento de la cría de conejos.
Para cualquier mes n, el número de conejos Fn estará dado por la relación de recurrencia Fn=Fn-1+Fn-2 con F0=0 y F1=1. Sus primeros términos son entonces: 0,1,1,2,3,5,8,13,21,34,55,89..... Para generar un nuevo término basta con sumar los dos que le anteceden.
En el video se muestra adicionalmente que esta es una sucesión monotona creciente no acotada y divergente.