Coordenadas cartesianas (1º ESO)
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 17:07 8 nov 2017 Coordinador (Discusión | contribuciones) (→Sistema de ejes cartesianos) ← Ir a diferencia anterior |
Revisión de 12:52 7 dic 2017 Coordinador (Discusión | contribuciones) (→Coordenadas cartesianas) Ir a siguiente diferencia → |
||
| Línea 109: | Línea 109: | ||
| |descripcion=Actividades para que puedas aprender a representar puntos del plano con respecto a unos ejes cartesianos. | |descripcion=Actividades para que puedas aprender a representar puntos del plano con respecto a unos ejes cartesianos. | ||
| |url1=http://genmagic.net/repositorio/displayimage.php?pos=-380 | |url1=http://genmagic.net/repositorio/displayimage.php?pos=-380 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 10a | ||
| + | |descripcion=Partes del plano cartesiano. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/a/coordinate-plane-parts-review | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 10b | ||
| + | |descripcion=Representación de puntos en el plano cartesiano. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/a/points-on-the-coordinate-plane | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Actividad 10c | ||
| + | |descripcion=Repaso de representación de puntos en el plano cartesiano. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/a/graphing-coordinates-review | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1a | ||
| + | |descripcion=Partes del plano cartesiano. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/e/graphing_points_2 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1b | ||
| + | |descripcion=Representación de puntos en el plano cartesiano. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/e/identifying_points_1 | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1c | ||
| + | |descripcion=Distancia entre puntos: vertical u horizontal. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/e/relative-position-on-the-coordinate-plane | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1d | ||
| + | |descripcion=Problemas del plano coordenado en los cuatro cuadrantes. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/e/coordinate-plane-word-problems | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1e | ||
| + | |descripcion=Reflejar puntos en el plano coordenado. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/e/reflecting-points | ||
| + | }} | ||
| + | {{AI_Khan | ||
| + | |titulo1=Autoevaluación 1f | ||
| + | |descripcion=Relaciones entre dos patrones. | ||
| + | |url1=http://es.khanacademy.org/math/pre-algebra/pre-algebra-negative-numbers/pre-algebra-coordinate-plane/e/visualizing-and-interpreting-relationships-between-patterns | ||
| }} | }} | ||
| {{AI_vitutor | {{AI_vitutor | ||
| |titulo1=Autoevaluación | |titulo1=Autoevaluación | ||
| |descripcion=Actividades de autoevaluación sobre coordenadas cartesianas. | |descripcion=Actividades de autoevaluación sobre coordenadas cartesianas. | ||
| - | |url1=https://www.vitutor.com/fun/1/a_1_e.html | + | |url1=http://www.vitutor.com/fun/1/a_1_e.html |
| }} | }} | ||
| }} | }} | ||
| [[Categoría: Matemáticas]][[Categoría: Funciones]] | [[Categoría: Matemáticas]][[Categoría: Funciones]] | ||
Revisión de 12:52 7 dic 2017
Introducción
Un toque divertido para empezar el tema:
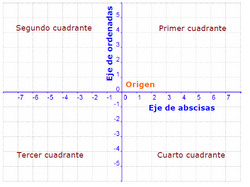
Sistema de ejes cartesianos
Su creador fue el filósofo y matemático francés Rene Descartes (Renatus Cartesius, en latín), de ahí el nombre.  |  |
Coordenadas cartesianas
| El propósito del sistema cartesiano es ubicar con facilidad distintos objetos. Se utiliza en la Física para ubicar vectores, en Geometría para ubicar puntos en el plano o en la aviación y navegación para saber la ubicación de un avión o un barco, así como cualquier punto en un territorio. También veremos que es útil para la representación de funciones en las que relacionamos dos variables, como por ejemplo, el tiempo y la distancia recorrida por un móvil.
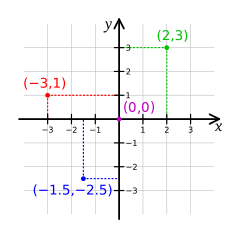
Para ubicar esos objetos utilizaremos su coordenadas. Veamos que es eso. Las coordenadas de un punto son un par ordenado de valores, (x,y):
|  |
