Plantilla:Ecuación de primer grado
De Wikipedia
| Revisión de 07:14 12 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 07:18 12 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 1: | Línea 1: | ||
| {{Caja_Amarilla|texto=Una '''ecuación de primer grado''' es una ecuación polinómica que, tras ser reducida (simplificada), sólo posee monomios de grado uno. Puede tener una incógnita, dos, etc. según el numero de variables que tenga el polinomio.{{p}} | {{Caja_Amarilla|texto=Una '''ecuación de primer grado''' es una ecuación polinómica que, tras ser reducida (simplificada), sólo posee monomios de grado uno. Puede tener una incógnita, dos, etc. según el numero de variables que tenga el polinomio.{{p}} | ||
| }} | }} | ||
| - | {{p}} | ||
| - | {{Caja_gris|texto='''Nota:''' Una ecuación de primer grado puede no parecerlo antes de reducirla. Será necesario operar y transponer términos antes de poder determinar el tipo de ecuación. Por ejemplo, la ecuación puede tener algunos monomios de grado 2 o superior pero conseguir que éstos desaparezcan tras reducirla, quedando sólo términos de grado 1.}} | ||
| {{p}} | {{p}} | ||
| {{Ejemplo_simple|titulo=Ejemplos:|contenido= | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| Línea 9: | Línea 7: | ||
| *<math>xy=x+y-3\;\!</math> (No es de primer grado, ya que el polinomio del miembro izquierdo tiene grado 2) | *<math>xy=x+y-3\;\!</math> (No es de primer grado, ya que el polinomio del miembro izquierdo tiene grado 2) | ||
| }} | }} | ||
| + | {{p}} | ||
| + | {{Caja_gris|texto='''Nota:''' Una ecuación de primer grado puede no parecerlo antes de reducirla. Será necesario operar y transponer términos antes de poder determinar el tipo de ecuación. Por ejemplo, la ecuación puede tener algunos monomios de grado 2 o superior pero conseguir que éstos desaparezcan tras reducirla, quedando sólo términos de grado 1.}} | ||
| + | {{p}} | ||
| + | {{Ejemplo_simple|titulo=Ejemplos:|contenido= | ||
| + | *<math>x^2+5x=x(x+1)+1\;\!</math> parece de segundo grado, pero al reducirla queda <math>4x-1=0\;\!</math> que es de primer grado.}} | ||
| {{p}} | {{p}} | ||
| ===Ecuación de primer grado con una incógnita=== | ===Ecuación de primer grado con una incógnita=== | ||
Revisión de 07:18 12 nov 2017
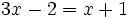 (Ecuación de primer grado con una incógnita)
(Ecuación de primer grado con una incógnita)
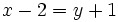 (Ecuación de primer grado con dos incógnitas)
(Ecuación de primer grado con dos incógnitas)
 (No es de primer grado, ya que el polinomio del miembro izquierdo tiene grado 2)
(No es de primer grado, ya que el polinomio del miembro izquierdo tiene grado 2)
Nota: Una ecuación de primer grado puede no parecerlo antes de reducirla. Será necesario operar y transponer términos antes de poder determinar el tipo de ecuación. Por ejemplo, la ecuación puede tener algunos monomios de grado 2 o superior pero conseguir que éstos desaparezcan tras reducirla, quedando sólo términos de grado 1.
Ecuación de primer grado con una incógnita
Solución de la ecuación de primer grado con una incógnita
Toda ecuación de primer grado con una incógnita se puede reducir a la forma:
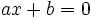
con 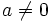 , cuya única solución es:
, cuya única solución es:
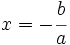
Nota: Si al reducir la ecuación de partida resulta que el coeficiente de primer grado es 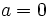 , entonces la ecuación de partida no es realmente de primer grado, sino de grado cero. Estos caso especiales los estudiaremos en otro apartado de este tema.
, entonces la ecuación de partida no es realmente de primer grado, sino de grado cero. Estos caso especiales los estudiaremos en otro apartado de este tema.
En la siguiente escena tienes ejemplos de soluciones de ecuaciones de primer grado con una incógnita.
Pulsa los botones para ver más ecuaciones.
Actividades en la que aprenderás a resolver ecuaciones de primer grado sencillas.
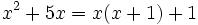 parece de segundo grado, pero al reducirla queda
parece de segundo grado, pero al reducirla queda 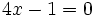 que es de primer grado.
que es de primer grado.

