Plantilla:Número de soluciones de una raíz cuadrada
De Wikipedia
(Diferencia entre revisiones)
| Revisión de 12:54 16 nov 2017 Coordinador (Discusión | contribuciones) ← Ir a diferencia anterior |
Revisión de 12:57 16 nov 2017 Coordinador (Discusión | contribuciones) Ir a siguiente diferencia → |
||
| Línea 30: | Línea 30: | ||
| |url1=http://maralboran.org/web_ma/Melide/Potencias_y_raices/Raices_cuadradas.html | |url1=http://maralboran.org/web_ma/Melide/Potencias_y_raices/Raices_cuadradas.html | ||
| }} | }} | ||
| - | }} | ||
| - | {{AI_melide | ||
| - | |titulo1=Raíces de otros índices (Ampliación) | ||
| - | |descripcion=Actividades sobre raíces de índice mayor que 2. | ||
| - | |url1=http://maralboran.org/web_ma/Melide/Potencias_y_raices/AMPLIACION_Raicesdeotrosindices.html | ||
| }} | }} | ||
Revisión de 12:57 16 nov 2017
Dependiendo del signo del número entero, su raíz puede existir o no. Tenemos los dos casos siguientes:
Número de soluciones de la raíz cuadrada
- La raíz cuadrada de un número entero positivo tiene dos soluciones iguales pero opuestas en signo, que no siempre son números enteros. (Ver: Raíz exacta y raíz entera de un número natural)
- La raíz cuadrada de un número entero negativo no existe.
Raíz cuadrada de un número entero. Ejemplos
- Actividad para aprender a calcular raíces de números enteros.
- Actividad para practicar las raíces de números enteros.
Actividades sobre raíces cuadradas exactas y enteras.
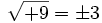
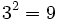
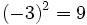
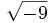 no existe, porque no hay níngún número cuyo cuadrado sea negativo, -9.
no existe, porque no hay níngún número cuyo cuadrado sea negativo, -9.

